Разбиение множеств

Понятие разбиения множества. Пусть А - множество учеников некой школы. Обозначим А₁ множество учеников первого класса, А₂ -множество учеников второго класса и т. д., А₁₀-множество учеников десятого класса этой школы. Ясно, что А₁А_2¼А₁₀- подмножество множества А, причем каждое из них не пусто ( в каждом классе, конечно, есть ученики), они попарно не имеют общих элементов (не может же один и тот же человек учиться одновременно в двух разных классах) и объединение всех равно А.

Говорят, что совокупность подмножеств множества М образует его разбиение , если каждое из этих подмножеств не пусто, любые два из них не имеют общих элементов и объединение всех их равно М.

Таким образом, в примере рассмотренном выше, совокупность подмножеств А₁,А₂¼А₁₀ образует разбиение множества А.

Если, например, А={1, 2, 3, 4, 5, 6}, то совокупность подмножеств {1, 3}, {2, 4, 6}, {5} множества А образует его разбиение, а его совокупность таких подмножеств {1,2,3},{4,5},{3,6} разбиения не образует, ибо два из них имеют общий элемент.

Итак, выражаясь образно , под разбиением множества мы будем понимать "разбиение" его на части , подмножества. Ясно ,что одно и тоже множество "разбить" на части можно по-разному. Так, например, если В={a, b, c, d, e, f},то совокупности его подмножеств {a, b, c},{d, e, f, g},и{a, b},{c, d},{e, f, g}образуют его разбиения, но различные т.е. В " разбито" на подмножества по-разному.

Разбиения будем обозначать строчными буквами греческого алфавита:r,s,d и т.д.

Классы разбиения. Пусть М-множество и r-некоторое его разбиение. Каждое из подмножеств совокупности, образующей разбиениеr, называется классом разбиения.

Так, например, если В={a, b, c, d, e, f, g} и r-разбиение множества В, образованное совокупностью его подмножеств {a, b}, {e, d, f}, {c}, {g},то каждое из этих подмножеств является классом данного разбиения r.

Если теперь изобразить множество с помощью диаграммы Эйлера-Венна, то его разбиение можно представить наглядно, в виде разорванного на части круга. Каждая такая часть и является классом данного разбиения.

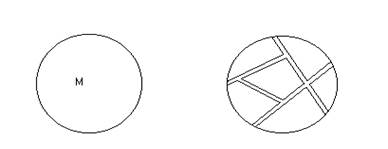
В одном и том же классе разбиения r множества М может содержаться несколько (и даже бесконечно много) элементов из М. Если элементы x, yÎМ принадлежат одному и тому же классу данного разбиения r , то этот факт мы будем обозначать следующим образом: x~y(r). Например, для рассмотренного выше разбиения s множества В можно записать a~b(s), d~e(s),¼, а запись c~d(s) неверна , ибо c и dпринадлежат различным классам разбиения s. Так как, элементы a и а, конечно , лежат в одном и том же классе разбиения, ибо это один и тот же элемент, то можно записать a~a(s). Аналогично b~b(s),c~c(s) и т. д.

Пусть далее для разбиения r множества М и некоторых x, y, zÎМ

имеет место x~y(r) и y~z(r) . Запись x~y(r) означает, что элементы x и y принадлежат одному и тому же классу нашего разбиения. Аналогично y и z содержаться в одном и том же классе. Если теперь предположить, что x и z лежат в различных классах разбиения r, то получим , что эти классы имеют общий элемент y, а это невозможно. Значит, x~z(r).

Таким образом, мы доказали, что если x~y(r)и y~z(r), то x~z(r).

Каждый класс данного разбиения r множества М, по определению, не пуст, т.е. в каждом классе содержатся элементы из М.

Например, для разбиения и s множества В, рассмотренных выше, класс разбиения {a, b} можно обозначить `a, ибо он содержит элемент a. Но этот же класс содержит и элемент b, значит, его можно обозначить `b. Таким образом , {a, b}=`a=`b. Аналогично {e, d, f}=`e=`d=`f.

У нас получилось, что один и тот же класс разбиения обозначается по-разному. Это не должно вас удивить. И в математике, и в жизни вы не раз встречались с такой ситуацией. Например, дроби 1/2, 2/4, 3/6,¼-это одно и то же число, обозначаемое по-разному.

Вернемся теперь к общему случаю разбиения r множества М. Если некоторый класс разбиения содержит элементы x и y множества М, то, с одной стороны, он обозначается `x, а с другой- `y, т. е. `x=`y. Таким образом, мы доказали, что из x~y(r) следует `x=`y.

Пусть теперь, наоборот, `x =`y. Но `x - это класс, содержащий элемент y, и эти классы равны, т. е. это один и тот же класс. Значит, x и y содержатся в одном и том же классе разбиения, т. е. x~y(r).

Из приведенных выше рассуждений мы можем сделать следующий вывод:`x =`y тогда и только тогда, когда x~y(r).

Фактор множества. Рассмотрим построенное выше разбиение s множества В. Подмножества {a,b},{e,d,f},{c},{g} являются классами этого разбиения. Согласно нашей договоренности, их можно обозначить, например, `a,`e,`c, `g соответственно. Таким образом, с разбиением s связана совокупность его классов разбиения, т. е. множество {`a,`e, `c,`g}.

И в общем случае, если r-некоторое разбиение произвольного множества М, то с этим разбиением связана совокупность его классов.

Совокупность всех классов данного разбиения r множества М называется фактор- множеством множества М по разбиению r и обозначается М/r.

Таким образом, элементами множества М/r являются классы данного разбиения rи других элементов в нем нет.

Если мы вернемся к разбиению r множества М, изображенному на рис. 10, то множество М/r состоит из кусков (рис. 1.8), на которые мы разрезали круг, изображающий множество М. Далее, для нашего разбиения s множество В имеем В/s = {`a, `e, `c, `g}. Конечно же, элементы множества В/s можно обозначить и по-другому, и тогда, например, В/s={b, f, c, g}.

М/r = , , , ,

Пусть теперь d - разбиение множества В, классами которого являются подмножества {a, b, c, d}, {e, f, g}.Тогда В/d={a, `e}.Обращаем ваше внимание на то, что `a в В/d и `a в В/d - это разные элементы, Например, кинотеатр "Мир" в Минске и кинотеатр "Мир" в Москве - это разные кинотеатры, и хотя они называются одинаково, это не вызывает недоразумений. Не будет их и в нашем случае с разбиениями, так как всегда ясно о каком разбиении идет речь.

Заметим. Что М/r - это совокупность лишь некоторых (не всех) подмножеств множества М, а 2^М-совокупность всех их. Значит, М/rÌ2^М, более того, М/r - собственное подмножество множества 2^М.

Ясно, что если множество М конечно, то и всякое его фактор -множество в зависимости от разбиения может быть как конечным, так и бесконечным. Вы без труда приведете соответствующие параметры.