Операции с множествами

Равенство множеств. Множества А и В равны тогда и только тогда, когда каждый элемент множества А является элементом множества В, и наоборот, каждый элемент множества В является элементом множества А, т. е.

А Ì В и В Ì А

Объединение множеств. Объединением или суммой двух множеств А и В называется множество, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств.

Выполняются законы:

S 1)Ассоциативный.

(АÈВ)ÈС=АÈ(ВÈС)=АÈВÈС.

А В 2) Коммутативный.

АÈВ=ВÈА; АÈА=А;

АÈÆ=А;

АÈS=S; АÈВ=А если В Ì А.

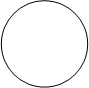
Пересечение множеств. Пересечением или произведением двух множеств называется множество, состоящие, из всех тех элементов, которые принадлежат обеим множествам.

S Справедлив коммутативный и

ассоциативный закон в частности:

А АÇ(ВÈС)=(АÇВ)È(АÇС).

В

Два множества А и В являются взаимоисключающими, или несовместимыми, если АÇВ=Æ.

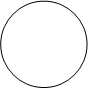
Дополнение множеств. Дополнение множества А называется множество, в котором содержатся все элементы пространства S^’, кроме принадлежащих множеству А. Оно обозначается через `А.

Справедливыми будут следующие

выражения

=

`А А `Æ=S; `S=Æ; (A)=A; AÈ`A=S;

AÇ`A=Æ;

`AÌ`B при ВÌА;

`A=`B если А=В.

Кроме того, справедливы законы де Моргана:

(АÈВ)=`А Ç`В; (АÇВ)=`А È`В.

Разность множеств. Разность А-В множеств А и В есть множество, состоящие из элементов множества А, не принадлежащих множеству В.

A - B=A \ B=A Ç`B=A - (AÇB).

A S (читаем “A без B”)

А-В

В

В-А

Из последней диаграммы выведены следующие соотношения:

А - Æ = А, А - S = Æ, S - A =`A.

Выражения, где присутствует разность, необходимо записывать со скобками.

Описанные выше операции со множествами проиллюстрируем примером. Предположим, что элементами пространства S – натуральные числа от 1 до 6. S={1, 2, 3, 4, 5, 6} и определим следующие подмножества:

А={2, 4, 6}; B={1, 2, 3, 4}; C={1, 3, 5}.

Учитывая приведенные соотношения можно записать:

(АÈВ)={1, 2, 3, 4, 6}, (BÈC)={1, 2, 3, 4, 5}

(AÈBÈC)={1, 2, 3, 4, 5, 6}=S=AÇC,

AÇB={2, 4}, BÇC={1, 3}, AÇC=Æ,

AÇBÇC=Æ,`A={1, 3, 5}=C, `B={5, 6},

`C={2, 4, 6}=A, A-B={6}, B-A={1, 3},

A-C={2, 4, 6}=A, C-A={1, 2, 5}=C,

B-C={2, 4}, C-B={5}.