Оценка параметров нормального распределения с помощью доверительных интервалов

Всякая статистическая оценка параметра, вычисленная по данным выборки, может быть только приближенной. Поэтому она может иметь определенный смысл лишь в том случае, когда указываются границы возможной погрешности оценки или, другими словами, указывается интервал, внутри которого с заданной вероятностью будет лежать истинное значение параметра. Этот интервал носит название доверительного, а границы его — доверительных границ.

Доверительные интервалы для оценки генеральной средней. Если генеральная совокупность имеет нормальное распределение, то как было указано ранее, величина 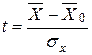для больших выборок также распределена нормально со средним значением 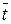= 0 и дисперсией Dt = 1. Поэтому для любого уровня значимости Р легко построить доверительные границы для неизвестного значения 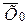, воспользовавшись неравенством:

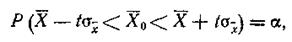
подставляя 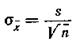, получим

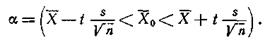
Величина t определяется по справочной таблице (приложения 1) по заданной вероятности a = 2Ф (t).

Значения 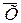± 0,196s являются доверительными границами для среднего значения генеральной совокупности при 5%-ном уровне значимости. Уровень значимости равен q = 1 — a = 1 — 0,95 = 0,05.

Если выборка имеет объем п £ 25, то величина t имеет распределение Стюдента. Поэтому в этом случае значение t определяется по таблице (приложения 2) по заданному значению a и k = п — 1.

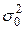Доверительные интервалы для оценки и a. Если генеральная совокупность имеет нормальное распределение, то величина 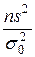имеет c²-распределение с числом степеней свободы k = п — 1. Здесь п — объем выборки и s² —дисперсия выборки.

Задавшись вероятностью a при определении доверительных границ для 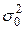и определив доверительный уровень значимости q = 1 — a, можно вычислить по c²-распределению величины 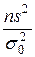два значения c²: одно для вероятности P₁ = 1-q/2, обозначим его 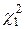и другое для вероятности Р₂ = q/2, обозначим его 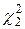. Тогда вероятность того, что величина 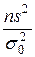окажется в границах от 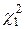до 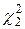будет равна a:

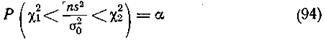
или с той же вероятностью можно ожидать выполнение следующих неравенств:

Для числа 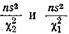определяют доверительные границы для 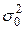. Значения c² для различных Р приведены в таблице.

Оценка для параметра 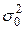с помощью доверительного интервала 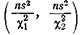дает в то же время доверительный интервал

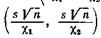для оценки параметра 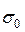с той же доверительной вероятностью a.