Оценка точности вычисления среднего квадратического отклонения генеральной совокупности по данным выборки

На практике иногда необходимо найти неизвестное среднее квадратическое отклонение генеральной совокупности s₀ по среднему квадратическому отклонению s малой выборки, когда ее объем п < 25. Для малых выборок s вычисляется по формуле

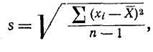
где в отличие от формулы (11) в знаменателе берется (п — 1), для того чтобы компенсировать систематическую ошибку, возникающую при оценке s₀ по s при малом числе п.

Эта задача сводится к определению вероятности a приближенного равенства s₀ » s, точность которого равна e:

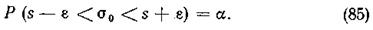
Если известно, что случайная величина х в генеральной совокупности подчинена нормальному закону распределения, то величина

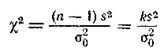
имеет распределение, которое носит название c²-распределения. Дифференциальная функция этого распределения или плотность вероятности величины c² имеет выражение

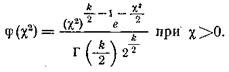
При помощи этой функции c²-распределения можно вычислить и вероятность a:

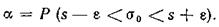
Для этой цели, полагая, что s - e > 0, преобразуем находящееся в скобках неравенство следующим образом:

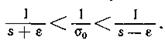
Умножим полученное неравенство на положительное число :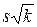

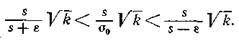
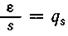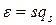Обозначив и , получим

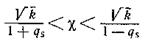
или

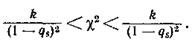
Вероятность этого неравенства равна интегралу

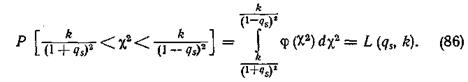
Но левая часть этого уравнения есть преобразованное выражение вероятности

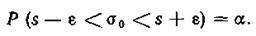
Следовательно, можно написать

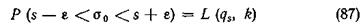
или

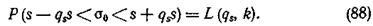
Значения интеграла L (q_sk) приведены в справочной таблице.

Необходимо заметить, что если s<e, то исходное неравенство для s₀

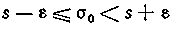
надо заменить неравенством

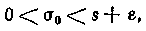
так как величина s₀ должна быть положительной. В этом случае неравенство для c примет вид

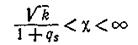
и вероятность его будет определяться интегралом

Значения этого интеграла также приведены таблице. При помощи таблицы значений вероятностей L (q_s, k) можно решать задачи трех типов:

1) по заданной точности e= q_s·s и объеме выборки п определить вероятность a приближенного равенства s₀ » s;

2) по заданной вероятности a приближенного равенства s₀ » s и объеме выборки п определить точность e= q_s·s этого равенства;

3) по заданной точности e и вероятности a приближенного равенства s₀ » s определить необходимый объем п выборки.