Нахождение корней уравнения

Рассмотрим решение уравнения вида f(x)=0.

Если f(x) является многочленом n-ой степени, т.е. уравнение имеет вид а_nxⁿ+а_n-1x^n-1+…+ а₁x+ а₀=0, то у него n корней. Все корни находятся в диапазоне [–k;k], где k вычисляется по формуле

k=max(|a_i|)/a_n.

Для нахождения корней с помощью Excel нужно:

1) Вычислить k;

2) Заполнить последовательность значений переменной х в диапазоне [–k;k] с каким-нибудь небольшим шагом;

3) Вычислить значение функции f(x) при каждом х (с помощью маркера заполнения);

4) Построить график функции f(x) (точечную диаграмму);

5) По графику функции или по таблице ее значений определить значения приближенных корней уравнения и ввести их в свободные ячейки ЭТ;

6) Вычислить значение функции от найденных приближенных значений корней уравнения;

7) Выполнить для каждого корня команду Сервис – Подбор параметра, установив в окне «Подбор параметра» следующие значения:

поле “Установить в ячейке” – ячейка со значением f(x),

поле “Значение” – 0,

поле “Изменяя значение ячейки” – ячейка со значением приближенного корня.

То есть добьемся того, чтобы значение функции f(x) равнялось нулю, подбирая точное значение корня х, близкое к приближенному значению.

Пример

Решить уравнение х³+х²–2х–1=0.

В нашем примере максимальный по модулю коэффициент уравнения равен 2, а коэффициент при х³ равен 1, следовательно, k=2, интервал, в котором лежат все корни уравнения, равен [–2;2].

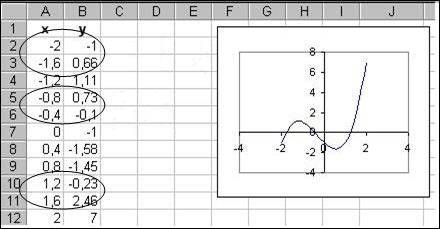
Составим таблицу значений функции y = х³+х²–2х-1, хÎ[–2;2] с шагом 0,4 и построим график этой функции.

По графику функции или по значениям функции в таблице можно определить интервалы, в которых лежат корни уравнения (по одному корню в каждом интервале). Если значения f(a) и f(b) функции f(х) имеют разные знаки, то в интервале [a;b] лежит корень уравнения f(х)=0. В нашем примере эти интервалы следующие: [–2;–1,6], [–0,8;–0,4], [1,2;1,6].

Запишем в качестве начальных приближений корней числа –1,8; –0,6 и 1,4 (середины найденных интервалов) в ячейки С2, С3 и С4. В ячейку D2 введем формулу =С2^3+C2^2-2*C2-1, скопируем эту формулу с помощью маркера заполнения в ячейки D3 и D4. Таким образом, мы вычислили значения функции y = х³+х²–2х–1 от приближенных значений корней этой функции.

Напомним, что если х₁ – корень функции y(x), то значение функции в корне – y(x₁) – равняется нулю.

Теперь выделим ячейку D2 и выполним команду Сервис – Подбор параметра горизонтального меню. В появившемся диалоговом окне запишем следующие: в поле “Установить в ячейке” введем D2, в поле “Значение” введем число 0, в поле “Изменяя значение ячейки” введем С2. То есть добьемся того, чтобы значение функции y(x) равнялось нулю, подбирая точное значение корня х, приближенное значение которого записано в ячейке С2.

Вводить ссылки на ячейки D2 и С2 в поля диалогового окна можно и с помощью мыши, щелкнув левой кнопкой мыши по соответствующей ячейке таблицы. При этом Excel автоматически превращает ссылки в абсолютные ($C$2).

После того как вы ввели все данные в диалоговом окне “Подбор параметра”, нажмите кнопку ОК, Excel найдет точное значение корня с учетом относительной погрешности и предельного числа итераций, которые вы установили ранее, и запишет его в ячейку С2.

Число 2,29Е-06 в ячейке D2 записано в экспоненциальной форме и означает 2,29×10^-6, то есть 0,00000229. Учитывая относительную погрешность 0,00001, можно сказать, что это ноль, следовательно, корень найден и он равен –1,80194.

Аналогично в ячейках С3 и С4 можно получить значения двух других корней нашего уравнения.

Итак, корни уравнения х³+х²–2х–1 = 0 равны:

х₁ = –1,80194; х₂ = –0,44504; х₃ = 1,24698.

Относительная погрешность вычислений и предельное число итераций задаются на вкладке “Вычисления” диалогового окна “Параметры”, открываемого командой Сервис – Параметры.Зададим относительную погрешность 0,00001 и предельное число итераций 1000.