Прямая и обратная геодезические задачи
Вычислительная обработка результатов измерений на местности, проводимая при составлении планов, решении ряда задач при проектировании сооружений и геодезической подготовке данных для выноса в натуру непосредственно связаны с решением прямой и обратной геодезических задач.
Прямая геодезическая задача. Сущность данной задачи: по известным координатам точки 1 (X1, X2) линии 1-2, дирекционному углу этой линии a1-2 и ее горизонтальному проложению d1-2 требуется определить координаты точки 2. проведя через точки 1 и 2 линии, параллельные координатным осям (рис. 4.3), получим прямоугольный треугольник 1-2’-2, в котором известна гипотенуза d1-2 и острый угол r = a1-2. Катеты этого треугольника являются приращениями координат DX и DY, которые могут быть получены по формулам:
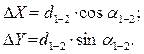
Тогда координаты искомой точки 2 определятся по формуле:
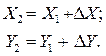
Приращения координат и координаты искомой точки вычисляются с точностью, соответствующей точности измерения горизонтальной длины линии.
Обратная геодезическая задача. По известным координатам точек 1 и 2 требуется определить горизонтальное проложение стороны d1-2 и дирекционный угол направления a1-2. Согласно рисунку 4.3 можно записать
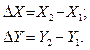
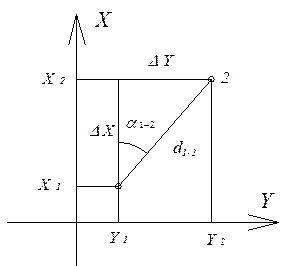
Рисунок 4.3 – Прямая и обратная геодезические задачи
По найденным значениям приращений координат DX и DY, решая прямоугольный треугольник, вычисляют табличный угол

По знакам приращений координат DX и DY определяют, в какой четверти лежит данное направление. Затем, руководствуясь соотношением между табличными и дирекционными углами (табл. 4.1), находят дирекционный угол направления. Зная дирекционный угол направления и приращения координат, определяют горизонтальное проложение стороны
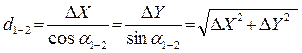
Дата добавления: 2015-10-05; просмотров: 1592;
