Тема 3: Теоремы сложения и умножения вероятностей
1. В урну, в которой лежат 6 белых и 5 черных шаров добавляют два черных шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что хотя бы один шар будет белым, равна …
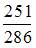
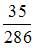
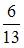
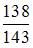
Решение:
Введем обозначения событий: 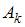 –
– 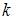 -ый вынутый шар будет белым, A – хотя бы один шар будет белым. Тогда
-ый вынутый шар будет белым, A – хотя бы один шар будет белым. Тогда 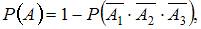 где
где 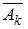 –
– 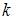 -ый вынутый шар не будет белым. Так как по условию задачи события
-ый вынутый шар не будет белым. Так как по условию задачи события 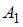 ,
, 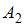 и
и 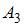 зависимы, то
зависимы, то
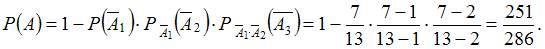
2. В урну, в которой лежат 6 белых и 5 черных шаров добавляют два белых шара. После этого наудачу по одному извлекают три шара без возвращения. Тогда вероятность того, что все три шара будут белыми, равна …
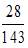
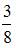
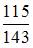
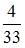
Решение:
Введем обозначения событий: 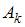 –
– 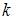 -ый вынутый шар будет белым, A – все три шара будут белыми. Тогда
-ый вынутый шар будет белым, A – все три шара будут белыми. Тогда 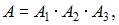 и так как по условию задачи события
и так как по условию задачи события 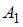 ,
, 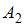 и
и 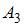 зависимы, то
зависимы, то
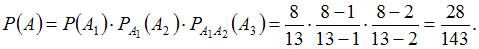
3. Вероятность поражения цели первым стрелком равна 0,95, а вторым – 0,80. Оба стрелка стреляют одновременно. Тогда вероятность того, что цель будет поражена только одним стрелком, равна …
0,23
0,95
0,875
0,17
Решение:
Введем обозначения событий: 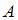 (цель поражена первым стрелком),
(цель поражена первым стрелком), 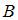 (цель поражена вторым стрелком). Так как эти события независимы, то искомую вероятность
(цель поражена вторым стрелком). Так как эти события независимы, то искомую вероятность 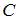 можно вычислить как:
можно вычислить как:
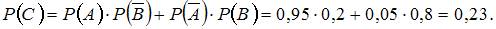
4. Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна 0,15; второй –0,05; третий –0,2. Тогда вероятность того, что в течение часа потребуют вмешательства наладчика все три станка, равна …
0,0015
0,4
0,015
0,9985
Решение:
Введем обозначения событий: 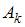 (вмешательства наладчика потребует
(вмешательства наладчика потребует 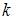 -ый станок),
-ый станок), 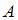 (вмешательства наладчика потребуют все три станка).
(вмешательства наладчика потребуют все три станка).
Тогда
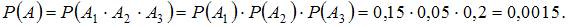
Дата добавления: 2015-09-29; просмотров: 7646;
