Приближенные вычисления с помощью полного дифференциала

Пусть функция 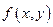дифференцируема в точке 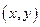. Найдем полное приращение этой функции:

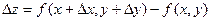или

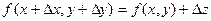
Если подставить в эту формулу выражение:

,

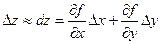то получим приближенную формулу:

.

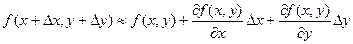Пример. Вычислить приближенно значение 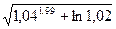, исходя из значения функци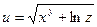и при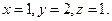

Из заданного выражения определяем 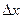= 1,04 – 1 = 0,04, 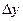= 1,99 – 2 = -0,01,

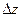= 1,02 – 1 = 0,02.

Находим значение функции = .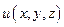

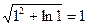Определяем частные производные:

; ; .

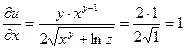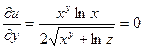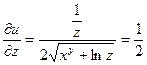Полный дифференциал функции 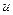равен:

.

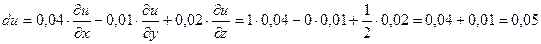
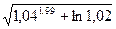
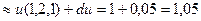Приведём точное значение этого выражения: 1,049275225687319176.