Экстремум функции нескольких переменных

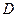Определение. Пусть функция определена в некоторой области , и 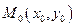- произвольная точка этой области. Если для всех точек 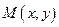из некоторой окрестности точки 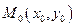выполняется неравенство:

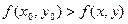
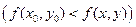
то точка 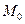называется точкой локального максимума (локального минимума) функции 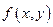в области .

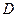Определение.Точки локального максимума и локального минимума функции 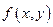называются точками экстремума этой функции.

Теорема.(Необходимые условия экстремума). Пусть функция 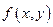непрерывна в некоторой области 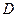вместе со своими первыми частными производными. Если во внутренней точке 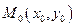области 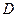функция 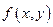имеет экстремум, то в этой точке обращаются в ноль все её частные производные первого порядка:

.

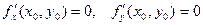Эта точка 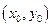называется критической точкой функции 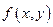в области .

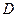Теорема. (Достаточные условия экстремума).

Пусть в окрестности критической точки 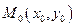функция 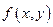имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

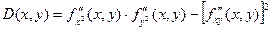
1) Если 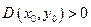, то в точке 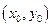функция 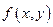имеет экстремум, если 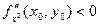- максимум, если 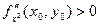- минимум.

2) Если 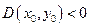, то в точке 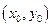функция 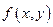) не имеет экстремума

В случае если 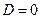, вывод о наличии экстремума сделать нельзя.