Производная по направлению. Рассмотрим функцию в точках и .
Рассмотрим функцию 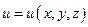 в точках
в точках 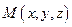 и
и 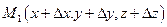 .
.
Построим вектор 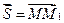 . Углы наклона этого вектора к положительным направлениям координатных осей
. Углы наклона этого вектора к положительным направлениям координатных осей 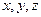 обозначим соответственно
обозначим соответственно 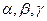 . Косинусы этих углов называются направляющими косинусамивектора
. Косинусы этих углов называются направляющими косинусамивектора 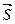 .
.
Расстояние между точками 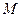 и
и 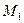 обозначим через
обозначим через 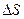 :
:
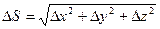 .
.
Высказанные выше предположения, проиллюстрируем на рисунке:
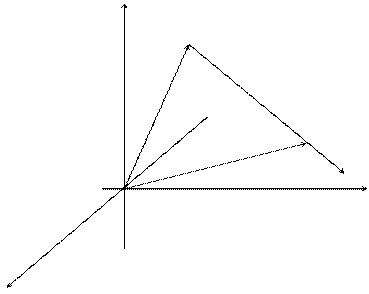 z
z
M
M1
y
x
Предположим, что функция 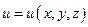 непрерывна и имеет непрерывные частные производные по переменным
непрерывна и имеет непрерывные частные производные по переменным 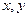 и
и 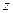 . Тогда справедливо равенство:
. Тогда справедливо равенство:
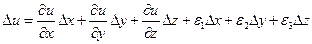 ,
,
где величины 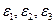 – бесконечно малые при
– бесконечно малые при 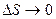 функции.
функции.
Из геометрических соображений очевидно:
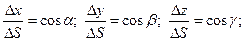
Таким образом, приведенные выше равенства могут быть представлены следующим образом:
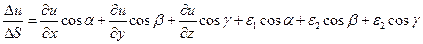 ;
;
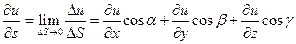 .
.
Величина 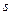 является скалярной. Она определяет направление вектора
является скалярной. Она определяет направление вектора 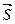 . Определение. Предел
. Определение. Предел 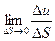 называется производной функции
называется производной функции 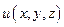 по направлению вектора
по направлению вектора 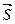 в точке с координатами
в точке с координатами 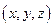 .
.
Пример. Вычислить производную функции 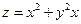 в точке
в точке 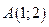 по направлению вектора
по направлению вектора 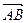 :
: 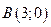 .
.
Решение. Определяем координаты вектора 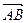 :
:
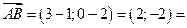 2
2 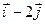 .
.
Находим модуль этого вектора:
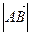 =
= 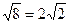 .
.
Находим частные производные функции 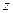 в общем виде:
в общем виде:
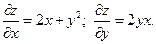
Значения этих величин в точке А равны: 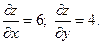
Для нахождения направляющих косинусов вектора 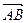 проведём преобразования:
проведём преобразования:
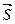 =
= 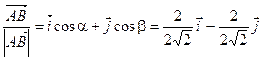
В качестве вектора 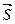 примем произвольный вектор, направленный вдоль заданного вектора, т.е. определяющего направление дифференцирования. Получаем значения направляющих косинусов вектора
примем произвольный вектор, направленный вдоль заданного вектора, т.е. определяющего направление дифференцирования. Получаем значения направляющих косинусов вектора 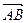 :
:
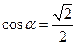 ;
; 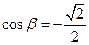 .
.
Окончательно находим: 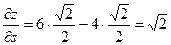 - значение производной заданной функции по направлению вектора
- значение производной заданной функции по направлению вектора 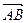 .
.
Дата добавления: 2015-09-29; просмотров: 754;
