Вычисление объемов тел вращения
Рассмотрим кривую, заданную уравнением 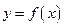 . Предположим, что функция
. Предположим, что функция 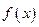 непрерывна на отрезке
непрерывна на отрезке 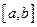 . Если соответствующую ей криволинейную трапецию с основаниями
. Если соответствующую ей криволинейную трапецию с основаниями 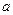 и
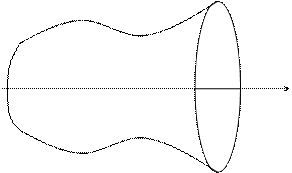
и 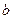 вращать вокруг оси Ох, то получим так называемое тело вращения.
вращать вокруг оси Ох, то получим так называемое тело вращения.
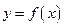
x
Каждое сечение тела плоскостью 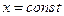 представляет собой круг радиуса
представляет собой круг радиуса 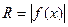 . Следовательно, объем тела вращения находится по полученной выше формуле:
. Следовательно, объем тела вращения находится по полученной выше формуле:
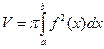 .
.
Дата добавления: 2015-09-29; просмотров: 953;
