Производных высших порядков
Пусть в точке 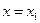
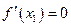 и
и 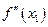 существует и непрерывна в некоторой окрестности точки
существует и непрерывна в некоторой окрестности точки 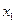 .
.
Теорема. Если 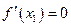 , то функция
, то функция 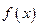 в точке
в точке 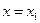 имеет максимум, если
имеет максимум, если  и минимум, если
и минимум, если  .
.
Доказательство. Пусть 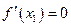 и
и  . Так как функция
. Так как функция 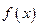 непрерывна, то
непрерывна, то 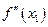 будет отрицательна в некоторой достаточно малой окрестности точки
будет отрицательна в некоторой достаточно малой окрестности точки 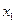 .
.
Так как 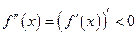 , то
, то 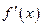 убывает на интервале, содержащем точку
убывает на интервале, содержащем точку 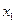 , но
, но 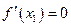 , т.е.
, т.е. 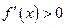 при
при 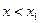 и
и 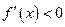 при
при 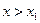 . Это и означает, что при переходе через точку
. Это и означает, что при переходе через точку 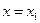 производная
производная 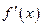 меняет знак с “+” на “-“, т.е. в этой точке функция
меняет знак с “+” на “-“, т.е. в этой точке функция 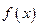 имеет максимум.
имеет максимум.
Для случая минимума функции теорема доказывается аналогично.
Если 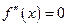 , то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
Дата добавления: 2015-09-29; просмотров: 643;
