Схема исследования функции и построение графика

Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо найти:

Область существования функции.

Это понятие включает в себя и область значений и область определения функции.

Точки разрыва. (Если они имеются).

Интервалы возрастания и убывания.

Точки максимума и минимума.

Максимальное и минимальное значение функции на ее области определения.

Области выпуклости и вогнутости.

Точки перегиба. (Если они имеются).

Асимптоты. (Если они имеются).

Построить график функции.

Применение этой схемы рассмотрим на примере.

Пример. Исследовать функцию 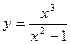и построить ее график.

Находим область определения функции. Очевидно, что областью определения функции является область .

Прямые являются вертикальными асимптотами кривой.

Областью значений данной функции является интервал .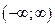

Точками разрыва функции являются точки .

Находим критические точки. Найдем производную функции:

.

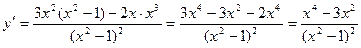Критические точки: ; ; ; .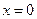

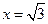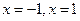Найдем вторую производную функции

.

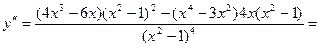
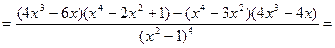
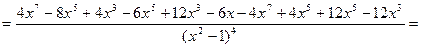
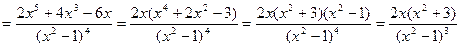Определим выпуклость и вогнутость кривой на промежутках.

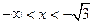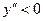, , кривая выпуклая;

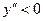, , кривая выпуклая;

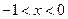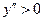, , кривая вогнутая;

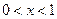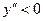, , кривая выпуклая;

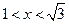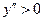, , кривая вогнутая;

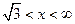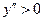, , кривая вогнутая.

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

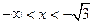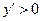, , функция возрастает;

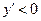, , функция убывает;

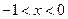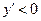, , функция убывает;

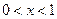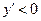, , функция убывает;

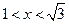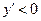, , функция убывает;

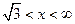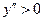, , функция возрастает.

Точка является точкой максимума, а точка 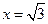является точкой минимума. Значения функции в этих точках равны соответственно 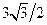и .

Найдем наклонные асимптоты.

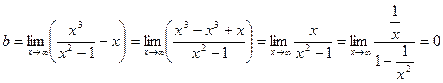
Следовательно, уравнение наклонной асимптоты – .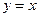

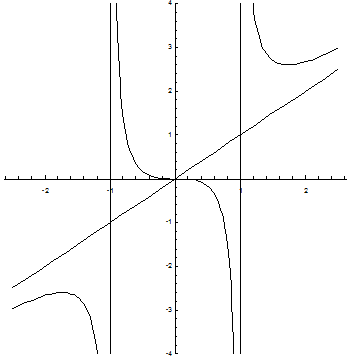
Построим график функции.