Уравнение прямой на плоскости, проходящей через две данные точки
Рассмотрим прямую в пространстве, проходящую через заданную точку 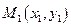 , с направляющим вектором
, с направляющим вектором 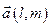 :
:
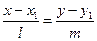 .
.
Пусть 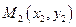 - произвольная точка этой прямой. Тогда выполняются равенства:
- произвольная точка этой прямой. Тогда выполняются равенства:
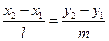 ,
,
Решая совместно эти уравнения, получим:
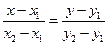
-уравнение прямой, проходящей через две точки 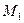 и
и 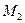 на плоскости.
на плоскости.
Замечание. Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
Пример. Найти уравнение прямой, проходящей через точки 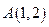 и
и 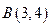 . Имеем
. Имеем
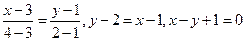 .
.
7. Уравнение прямой в отрезках
Если в общем уравнении прямой 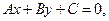
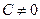 то, разделив на
то, разделив на 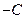 , получим:
, получим: 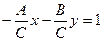 или
или 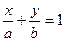 , где
, где 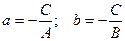 .
.
Геометрический смысл коэффициентов: коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой 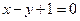 . Найти уравнение этой прямой в отрезках.
. Найти уравнение этой прямой в отрезках.
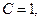
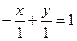 ,
, 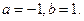
Дата добавления: 2015-09-29; просмотров: 933;
