Способы математических доказательств

Доказать какое-либо утверждение - это значит показать, что это утверждение логически следует из системы истинных и связанных с ним утверждений.

По способу ведения (т.е. по форме) различают: прямые и косвенные доказательства.

Прямые доказательства строятся на основе дедуктивных умозаключений.

К косвенным относятся доказательства методом от противного и доказательство на основе закона контрапозиции.

Для доказательства теоремы используйте схемы дедуктивных умозаключений.

Задание 1. Доказать, что в прямоугольнике диагонали равны.

Дано:

Доказать:

Док-во:

Сущность метода от противного заключается в следующем:

-пусть требуется доказать теорему А Þ В ;

- допускаем, что заключение теоремы (В ) - ложно, следовательно его отрицание 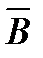-истинно;

-присоединяем предложение 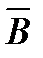условию;

-строим цепочку дедуктивных умозаключений до тех пор, пока не получим утверждение, противоречащее условию;

-делаем вывод о том, что полученное противоречие доказывает истинность теоремыА Þ В.

Задание 2. Доказать методом от противного, что если х 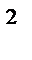- четное число, то и х - четное число.

Дано:

Доказать:

Док-во:

Задание 3. Доказать методом, основанным на законе контрапозиции. Если дробь 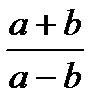несократима, то и дробь 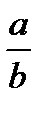тоже несократима.

Дано:

Доказать:

Док-во:

Задание 4. Доказать, методом полной индукции, что если натуральное число n не кратно 3, то значение выражения n 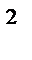+2 кратно 3.

Дано:

Доказать:

Док-во: