Расчет изменения энтропии процессов расширения и сжатия идеального газа при различных условиях
| Постоянный параметр | p | T | V | Q |
| ΔS |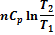 
| 
| 
| 
|
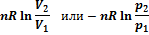
Если в системе, состоящей из идеального газа, изменяется несколько параметров, то, например, для изобарно-изотермического процесса:
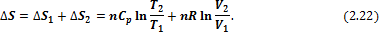
4) Смешение идеальных газов при постоянных температуре и давлении
Если n1 молей одного газа, занимающего объем V1, смешиваются с n2 молями другого газа, занимающего объем V2, то общий объем будет равен V1 + V2, причем газы расширяются независимо друг от друга и занимают весь объем, поэтому общее изменение энтропии равно сумме изменений энтропии каждого газа:
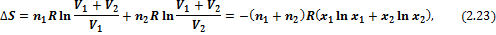
где 
– мольная доля i-го газа в полученной газовой смеси. Изменение энтропии (3.23) всегда положительно, так как все 
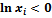, поэтому идеальные газы всегда расширяются необратимо.
5) Изменение энтропии при химической реакции
При постоянной температуре и давлении изменение энтропии может быть рассчитано как термодинамическая сумма мольных абсолютных стандартных энтропий веществ, участвующих в реакции:
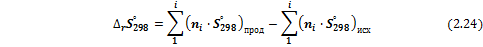
Изменение энтропии в ходе химической реакции при произвольной температуре рассчитывают по уравнению:
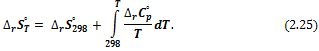
можно выразить как функцию температуры, используя температурные ряды теплоемкости; если известны средние теплоемкости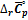 
можно вынести за знак интеграла.
Изменение энтропии изолированной системы включает в себя два слагаемых: изменение энтропии процесса (ΔSпр.) и изменение энтропии теплового источника (ΔSт.ист.), который входит в систему для исключения возможности обмена ее энергией с окружающей средой. Тогда:
Важно отметить, что только эта суммарная величина позволяет предвидеть направление самопроизвольного процесса.
Статистическое определение энтропии основано на идее о том, что необратимые процессы в термодинамике вызваны переходом системы в более вероятное состояние, поэтому энтропию можно связать с вероятностью:
где k – постоянная Больцмана (k = R/NA), W – так называемая термодинамическая вероятность, т.е. число микросостояний, которые соответствуют данному макросостоянию системы. Формулу (2.27) называют формулой Больцмана.
Вероятность W какого-либо состояния равняется числу всех возможных сочетаний, посредством которых может быть реализовано данное состояние. С увеличением количества молекул и числа доступных уровней энергии термодинамическая вероятность резко увеличивается, так что для обычных молекулярных систем при повышении температуры и разупорядоченности энтропия возрастает. Верно и обратное.
Во многих случаях изменение энтропии процесса можно оценить качественно, основываясь на следующих соображениях:
- Энтропия всегда увеличивается при переходе из конденсированного состояния (твердого или жидкого) в парообразное.
- Энтропия возрастает при растворении твердого или жидкого вещества, причем чем больше степень диссоциации, тем заметней увеличивается энтропия. При растворении газов, напротив, энтропия уменьшается.
- Энтропия данного количества вещества увеличивается по мере усложнения молекул. Например, S(СO) < S(СО2).
- Для газообразных веществ энтропия зависит от массы частиц и их геометрического строения. Так, S(CO2) < S(NO2), поскольку при практически одинаковых молекулярных массах молекула СО2 имеет линейное строение в отличие от NO2.
- В химических реакциях энтропия возрастает, если в результате их увеличивается количество газообразных веществ.
- Энтропия системы увеличивается с ростом температуры.
2.
Дата добавления: 2015-09-29; просмотров: 1860;