Энтропия.

Первый закон термодинамики позволяет определить энергетические характеристики химических реакций, что имеет важное значение как для теории химических процессов, так и для химической технологии. Второй закон термодинамики дает возможность разделить все допускаемые первым законом термодинамики процессы на самопроизвольно и несамопроизвольно протекающие в данных условиях.

Наиболее общими формулировками второго закона термодинамики являются: постулат Клаузиуса – «невозможен самопроизвольный переход теплоты от холодного тела к горячему», а также принцип качественной неэквивалентности теплоты и работы – любая форма энергии может полностью преобразоваться в теплоту, но теплота преобразуется в иные формы энергии лишь частично.

Взаимосвязь между работой и теплотой (тепловые машины, цикл Карно) описывается уравнением:

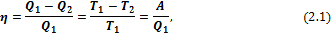
отсюда следует:

где η – коэффициент полезного действия (КПД); А – работа, совершенная системой; Q₁ – теплота, сообщенная системе при Т₁ (отдаваемая нагревателем); Q₂ – количество теплоты, отданное системой при Т₂ холодильнику.

Из уравнения цикла Карно Клаузиус вывел понятие об энтропии как функции состояния. Математическим выражением второго закона термодинамики является неравенство Клаузиуса:

где знак равенства относится к обратимому процессу, а знак неравенства – к необратимому.

Величина dS характеризует происходящее в системе изменение. Таким образом, второй закон термодинамики устанавливает критерий направленности термодинамических процессов – «энтропия (S) изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума». В изолированной системе (V, U = const) энтропия является критерием направленности самопроизвольного процесса и состояния равновесия:

Основное свойство энтропии: в обратимом процессе при переходе системы из состояния 1 в состояние 2 изменение энтропии определяется по уравнению:

или после интегрирования:

где δQ – элементарное количество теплоты, поглощенной или выделенной при обратимом процессе. Размерность энтропии Дж/(моль·К).

В связи с тем, что энтропия является функцией состояния, ее изменение при протекании как обратимого, так и необратимого процесса одинаково, поэтому для определения конечного изменения энтропии необходимо пользоваться математическими формулами для обратимых процессов (2.5) – (2.6).