Энтропия. Вероятностная трактовка.

Макроскопическое и микроскопическое описание объектов природы. Различные объекты и явления природы (системы) могут быть описаны как на микро-, так и на макроуровне, на основе их микросостояния или макросостояния. Сами понятия микро- и макро- отражают в какой-то степени наши представления о размерах объектов природы.

Макросостояние. Состояние макроскопического тела (системы), заданное с помощью макропараметров (параметров, которые могут быть измерены макроприборами – давления, температуры, объемом и другими макроскопическими величинами, характеризующими систему в целом), называют макросостоянием.

Микросостояние. Состояние макроскопического тела, охарактеризованное настолько подробно, что заданы состояния всех образующих тело молекул, называется микросостоянием.

Термодинамика, как уже говорилось, рассматривает тепловые процессы в системах на макроскопическом уровне, оперируя макропараметрами: температура, теплота, давление, объем. Статистическая физика, или молекулярно-кинетическая теория рассматривает тепловые явления на микроуровне – с точки зрения движения молекул – их скорости, кинетической энергии. Термодинамика, опираясь на понятие энтропии, четко различает обратимые и необратимые процессы. Способна ли не это статистическая физика? Другими словами, существует ли понятие аналогичное энтропии для микросостояния? Утвердительно ответить на этот вопрос позволили работы великого австрийского физика Людвига Больцмана, в которых отличие обратимых процессов от необратимых было сведено с макроскопического уровня на микроскопический.

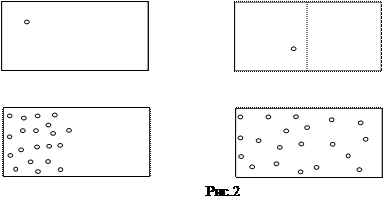Проведем вслед за Л. Больцманом мысленный эксперимент. Выделив некоторую молекулу в сосуде с теплоизолированными стенками (рис.2) и наблюдая за ней, мы убедимся, что она может занимать любой положение в сосуде. Если же мысленно разделить объем на две половины. В этом случае молекула, беспорядочно блуждая, сталкиваясь с другими молекулами, пробудет в одной половинке сосуда ровно половину времени, в течение которого мы ее наблюдаем. В этом случае говорят, что вероятность ее пребывания в одной из половинок сосуда равна ½. Вероятность может принимать значения от 0 до 1. Если же мы будет наблюдать уже за двумя мечеными молекулами, то вероятность того, что мы обнаружим сразу обе молекулы в одной половинке сосудаю, равна 1/2×1/2=1/4. Аналогично, для трех молекул эта вероятность (обозначим ее W) равна (1/2)³_, а для N молекул W=(1/2)^N. Т.е. вероятность стремительно падает. Таким образом, такое событие является маловероятным. Это понятно нам и на основе нашего жизненного опыта. Странно было бы, если бы все молекулы воздуха вдруг собрались бы в одной половине комнаты, а в другой образовалось безвоздушное пространство. Вероятность же того, что все молекулы находятся во всем объеме сосуда максимальна и равна 1. Число способов, которыми это состояние может быть реализовано, или статистический вес является также максимальным.

Пусть в некоторый момент времени удалось загнать все молекулы в правую верхнюю часть сосуда, отделенную диафрагмой. Остальные ¾ этого объема остались пустыми. После того как мы уберем диафрагму молекулы равномерно заполнят весь объем сосуда, т.е. перейдут из состояния с меньшей вероятностью в состояние с большей вероятностью. Таким образом, мы и здесь можем сказать, что процессы в системе идут только в одном направлении: от некоторой структуры (порядка, когда молекулы содержались в верхнем правом углу объема сосуда) к полной симметрии (хаосу, беспорядку, когда молекулы могут занимать любые точки пространства сосуда). Последнее состояние можно назвать состоянием равновесия. Все это наволит на мысль, что должна существовать связь между вероятностью и энтропией.

Если мы рассмотрим две подсистемы какой либо системы, каждая из которых характреизуется своим статистическим весом (вероятностью состояния) W₁ и W₂, то полный статистический вес системы равен произведению статистических весов подсистем:

W = W₁×W₂,

а энтропия системы S равна сумме энтропии подсистем S = S₁ + S₂.

Это наталкивает на мысль, что связь вероятности (статистического веса) и энтропии должна выражаться через логарифм:

Ln W = Ln (W_1×W₂) = Ln W₁ + Ln W₂ = S₁ + S₂ .

Собственно, это и сделал Больцман, связав понятие энтропии S c Ln W. Уже позднее, в 1906 г. Макс Планк написал формулу, выражающую основную мысль Больцмана об интерпретации энтропии как логарифма вероятности состояния системы:

S = k Ln W.

Эта формула выгравирована на памятнике Больцману на венском кладбище.

Коэффициент пропорциональности k был рассчитан Планком и назван им постоянной Больцмана.