Метод Эйлера. Метод Эйлера изучает определенную область движения жидкости

Метод Эйлера изучает определенную область движения жидкости. В этой области пространства фиксируются точки, которые являются неподвижными при прохождении через них жидкости. В этом случае не рассматриваются траектории движения частиц, как в методе Лагранжа. Метод Эйлера позволяет исследовать изменение скоростей, ускорений в разных точках выбранной области пространства жидкости. Скорости рассматриваются относительно неподвижной системы координат. Составляющие абсолютной скорости 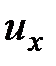, , 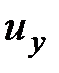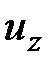зависят от нахождения точки в пространстве, т.е. от координат 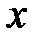, , 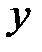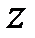и времени .

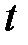Составляющие скорости выражаются следующими функциональными зависимостями:

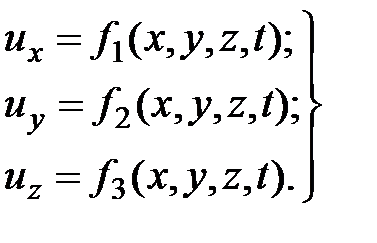(3.3)

Следует отметить, что давление в точке также является функцией координат:

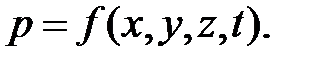(3.4)

Метод Эйлера позволяет получить распределение скоростей в определенной области. В случае движения жидкости, когда скорости частиц, проходящих через определенную точку в пространстве, зависят не только от координат расположения точки 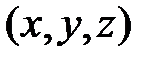, но и времени 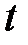(формула (3.3)), такое движение называется неустановившимся (нестационарным).

Установившимся (стационарным) движением является движение, когда скорости в точке не зависят от времен. Зависимости, определяющие скорости, в этом случае выглядят так:

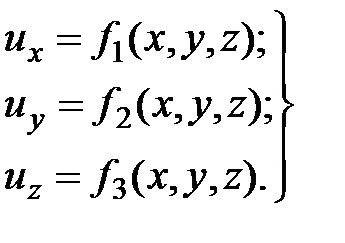(3.5)

Так как абсолютная скорость 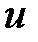является функцией координат 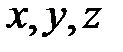и времени 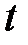, то полный дифференциал скорости в местных производных

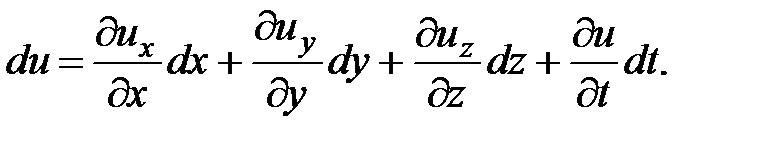(3.6)

Абсолютное ускорение в точке

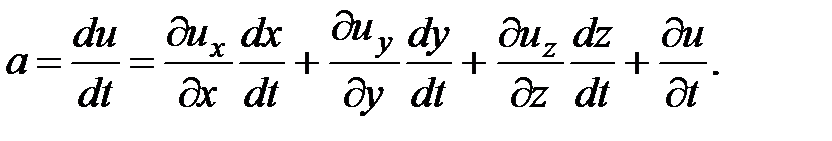(3.7)

Составляющие скорости

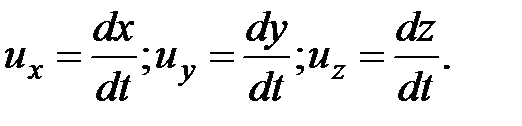(3.8)

При исследовании движения жидкости по методу Эйлера ее геометрическими характеристиками являются линии тока.

Частичка жидкости при движении может изменять свою форму при сохранении своего объема и массы. Частица может двигаться поступательно или вращательно, при этом по сравнению с твердым телом она деформируется.