ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ СТРУЙЧАТОЙ МОДЕЛИ ДВИЖЕНИЯ ЖИДКОСТИ

Как уже отмечалось ранее, пространство, заполненное жидкостью, состоит из бесконечного множества отдельных частиц жидкости, имеющих бесконечно малые размеры и массы. В определенной точке рассматриваемого пространства частица движется с определенной скоростью и на нее действует некоторое давление. При перемещении частицы в пространстве скорость и давление будут непрерывно изменяться. В определенный момент времени в рассматриваемом пространстве в разных его точках скорость имеет разное значение. Картина изменения скорости в пространстве характеризуется полем скоростей, изменение давления - полем давления.

Выделим в пространстве движущейся жидкости частицу жидкости. За определенный промежуток времени частица пройдет через ряд точек пространства с различными скоростями. След, оставленный частицей в виде кривой линии, является траекторией движения. При установившемся движении скорость в каждой точке траектории является неизменной во времени, а траектории отдельных частиц также являются во времени неизменными кривыми. При установившемся движении поле скоростей в рассматриваемом пространстве остается неизменным с течением времени.

В случае неустановившегося движения частица при прохождении точки в разное время имеет разные скорости.

Выберем в пространстве, занятом движущейся жидкостью, в некоторый момент времени 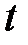т. 1, через которую пройдет частица жидкости. Построим к точке вектор скорости 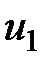, который определяет направление движения частицы и ее скорость. На этом векторе, отложив малое расстояние 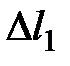, получим т. 2 (рис. 3.1).

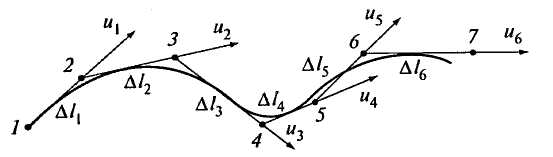
Рис. 3.1. Линия тока

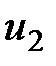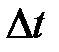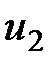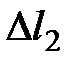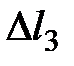В т. 2 построим вектор , соответствующий скорости частицы в данной точке через промежуток времени . На векторе отметим т. 3, отстающую на расстояние . В т. 3 также построим вектор , и на нем отложим расстояние и т.д. Если расстояния между точками 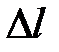будут стремиться к нулю, то в пределе получим кривую вместо ломаной линии 1, 2, 3, 4, ..., 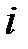. Полученная кривая, начинающаяся в т. 1, является линией тока.

Кривая, проведенная через ряд точек жидкости при установившемся ее движении, в каждой точке которой в данный момент времени 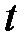векторы скорости касательные, называется линией тока. Линия тока в другой промежуток времени при неустановившемся движении будет представлять другую кривую.

В случае установившегося движения частицы жидкости будут перемещаться вдоль неизменной линии тока. Следовательно, при установившемся движении линии тока и траектории частиц совпадают.

Выделим в пространстве движущейся жидкости элементарный замкнутый контур и через все его точки проведем линии тока. Образовавшаяся таким образом трубчатая поверхность называется трубкой тока. Трубка тока представляет собой как бы бесконечно тонкую непроницаемую стенку.

Частички жидкости, движущиеся внутри трубки тока, образуют элементарную струйку жидкости. В случае стремления поперечных сечений струйки жидкости к нулю она в пределе будет обращаться в линию тока.

При установившемся движении элементарной струйки отмечают следующие ее свойства:

• форма элементарной струйки с изменением времени остается постоянной, так как линии тока, образующие трубку тока, не меняются во времени;

• поверхность трубки тока является непроницаемой для частичек жидкости, находящихся как в пределах струйки, так и вне ее;

• скорости движения частиц в разных точках малого поперечного сечения струйки 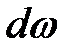считаются постоянными, как и давление в сечении.

По длине струйки форма, элементарные поперечные площади и скорости в них изменяются.

Поток жидкости в «струйчатой модели жидкости» рассматривается как совокупность элементарных струек, обладающих приведенными выше свойствами.

В потоке жидкости в связи с различием скоростей в соответствующих струйках они будут скользить относительно друг друга, при этом не будет происходить их перемешивания.