Шаровой сектор

Шаровым сектором называется геометрическое тело, полученное при вращении кругового сектора (с углом меньше 90°) вокруг оси, содержащей один из боковых радиусов. Дополнение такого тела до шара также называется шаровым сектором. Таким образом, шаровой сектор состоит из шарового сегмента и конуса, либо из шарового сегмента без конуса (рис. 12.43 а, б).

а) б)

Рис. 12.43

Для шарового сектора верны формулы:

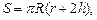
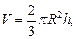
где S – площадь поверхности шарового сектора; R – радиус шара; r – радиус основания сегмента; h – высота шарового сегмента; V – объем шарового сектора.

Пример 1. Радиус шара разделили на три равные части. Через точки деления провели два сечения, перпендикулярные радиусу. Найти площадь сферического пояса, если радиус шара равен 15 см.

Решение. Сделаем рисунок (рис. 12.44).

Рис. 12.44

Для того чтобы вычислить площадь сферического пояса, надо знать радиус шара и высоту. Радиус шара известен, а высоту найдем, зная, что радиус разделен на три равные части: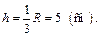

Тогда площадь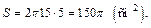

Пример 2.Шар пересечен двумя параллельными плоскостями, проходящими перпендикулярно диаметру и по разные стороны от центра шара. Площади сферических сегментов равны 42p см² и 70p см². Найти радиус шара, если расстояние между плоскостями равно 6 см.

Решение.Рассмотрим два сферических сегмента с площадями: 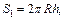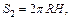где R – радиус шара (сферы), h, H – высоты сегментов. Получим уравнения: 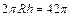и И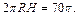меем два уравнения с тремя неизвестными. Составим еще одно уравнение. Диаметр шара равен 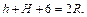Решим систему:

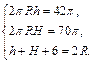
Из двух первых уравнений системы выражаем:

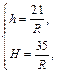
подставляем в третье уравнение системы: 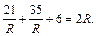Решаем полученное уравнение: 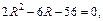получаем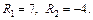

По условию задачи подходит значение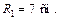

Пример 3.Сечение шара плоскостью, перпендикулярной его диаметру, делит диаметр в отношении 1 : 2. Во сколько раз площадь сечения меньше площади поверхности шара?

Решение. Сделаем рисунок (рис. 12.45).

Рассмотрим диаметральное сечение шара: AD – диаметр, O – центр, OE=R – радиус шара, BE – радиус сечения, перпендикулярного диаметру шара,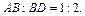

Выразим BE через R: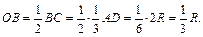

Из D OBE выразим BE через R:

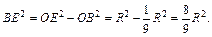
Рис. 12.45

Площадь сечения 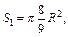площадь поверхности шара 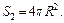Получаем отношение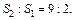

Следовательно, S₁меньше S₂в 4,5 раза.

Пример 4.В шаре, радиус которого 13 см, проведены два взаимно перпендикулярных сечения на расстоянии 4 см и 12 см от центра. Найти длину их общей хорды.

Решение.Сделаем рисунок (рис. 12.46).

Рис. 12.46

Сечения перпендикулярны, так как 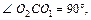OO₂ – расстояние и OO₁ – расстояние. Таким образом, 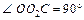и 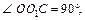OC – диагональ прямоугольника OO₂CO₁ и равна

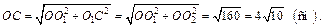
D O₁AB – равнобедренный (O₁A = O₁B – радиусы), тогда перпендикуляр O₁C является и медианой AC = CB.

Рассмотрим D OAC: OA – радиус шара, 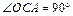(OC^AC по теореме о трех перпендикулярах). Находим:

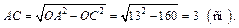
Общая хорда сечений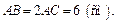

Получаем ответ: 6 см.

Пример 5. Площадь осевого сечения шарового сектора в три раза меньше площади большого круга шара. Найти отношение объемов сектора и шара.

Решение. Сделаем рисунок (рис. 12.47).

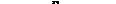
Рис. 12.47

Рассмотрим осевое сечение шара. Осевое сечение шарового сектора – это круговой сектор, площадь которого составляет 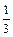площади круга. Значит, центральный угол равен 120°, следовательно, 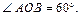Шаровой сектор можно рассматривать как тело, полученное при вращении сектора АОВ вокруг бокового радиуса ОВ. Высотой данного сектора служит отрезок СВ. Объем сектора вычисляется по формуле 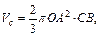объем шара –

Из DАОС ( 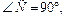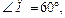ОА – радиус) выразим 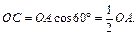Таким образом, 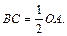Следовательно, 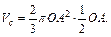Сравнивая объемы сектора и шара, получаем, что V_c : V_ш = 1 : 4.

Получаем ответ: 1 : 4.