Шар и сфера

Сферой называется множество всех точек пространства, равноудаленных от данной точки.

Данная точка называется центром сферы. Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы. Хордой называется отрезок, соединяющий две точки сферы. Диаметром называется хорда, проходящая через центр сферы (рис. 12.40).

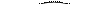
Рис. 12.40

Шаром называется геометрическое тело, ограниченное сферой. Центр, радиус, хорда и диаметр сферы называются соответственно центром, радиусом, хордой и диаметром шара (рис. 12.40).

Шар можно рассматривать как тело, полученное при вращении полукруга вокруг оси, содержащей диаметр полукруга.

Сферой также называется поверхность шара.

Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью к сфере (шару). Общая точка называется точкой касания сферы (шара) и плоскости.

Теорема. Для того чтобы плоскость была касательной к сфере (шару), необходимо и достаточно, чтобы эта плоскость была перпендикулярна к радиусу сферы (шара), проведенному в точку касания.

Для шара верны формулы:

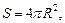
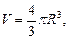
где S – площадь поверхности шара (площадь сферы); R – радиус шара; V – объем шара.