Многогранники и тела вращения
Цилиндр называется описанным около призмы, если окружности оснований цилиндра описаны около оснований призмы, а боковые ребра призмы являются образующими цилиндра. Призма соответственно называется вписанной в цилиндр.
Теорема. Для того чтобы около призмы можно было описать цилиндр, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.
Цилиндр называется вписанным в призму, если окружности его оснований вписаны в основания призмы, а боковая поверхность касается боковых граней призмы.
Теорема. Для того чтобы в призму можно было вписать цилиндр, необходимо и достаточно, чтобы призма была прямая и в ее основание можно было вписать окружность.
Конус называется описанным около пирамиды, если окружность основания конуса описана около основания пирамиды, а боковые ребра пирамиды являются образующими конуса. Пирамида соответственно называется вписанной в конус.
Теорема. Для того чтобы около пирамиды можно было описать конус, необходимо и достаточно, чтобы боковые ребра пирамиды были равны.
Конус называется вписанным в пирамиду, если окружность его основания вписана в основание пирамиды, а боковая поверхность касается боковых граней пирамиды. Пирамида соответственно называется описанной около конуса.
Теорема. Для того чтобы в пирамиду можно было вписать конус, необходимо и достаточно, чтобы в основание пирамиды можно было вписать окружность, а вершина пирамиды ортогонально проектировалась в центр этой окружности.
Пример 1. Шар вписан в прямую призму, основанием которой является прямоугольный треугольник с катетом a и противолежащим ему острым углом α. Найти объем призмы.
Решение. Сделаем рисунок (рис. 12.48). Шар вписан в прямую призму, значит, высота призмы равна диаметру шара, а в треугольник основания вписана окружность, радиус которой равен радиусу шара. Рассмотрим прямоугольный треугольник ABC, у которого катет BC = a, противолежащий ему ÐBAC = α. Найдем катет AC и гипотенузу AB:
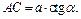
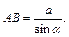

Рис. 12.48
Площадь треугольника ABC равна:
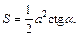
Вычислим радиус окружности, вписанной в треугольник:
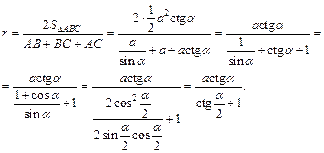
Вычисляем объем призмы по формуле
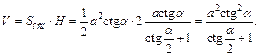
Получаем ответ: 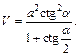
Пример 2. Боковое ребро правильной четырехугольной пирамиды равно a. Двугранный угол, образованный смежными боковыми гранями, равен β. Найти радиус шара, описанного около этой пирамиды.
Решение. Сделаем рисунок (рис. 12.49): ABCD – квадрат, SO – высота пирамиды, ÐAEC = b – двугранный угол.
Рассмотрим диагональное сечение пирамиды – треугольник SBD (SB = SD). Радиусом шара, описанного около данной пирамиды, будет радиус окружности, описанной около треугольника SBD. Найдем его по формуле
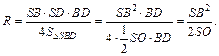

Рис. 12.49
Из подобия треугольников 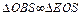 (ÐSOB = ÐSEO = 90°, ÐBSO = ÐOSE) следует пропорциональность сторон: SB/SO = BO/OE.
(ÐSOB = ÐSEO = 90°, ÐBSO = ÐOSE) следует пропорциональность сторон: SB/SO = BO/OE.
Из треугольника 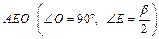 найдем
найдем 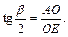 Так как АО = ВО, то
Так как АО = ВО, то 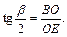 Следовательно,
Следовательно, 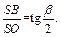
Вычисляем радиус окружности:
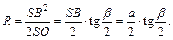
Получаем ответ: 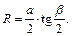
Пример 3.В усеченный конус вписан шар радиуса R. Образующая конуса наклонена к плоскости основания под углом a. Найти объем усеченного конуса.
Решение. Рассмотрим осевое сечение конуса (рис. 12.50).

Рис. 12.50
Введем обозначения: R1 – радиус нижнего основания конуса, R2 – радиус верхнего основания. Высота данного усеченного конуса будет равна диаметру вписанного в него шара 2R. Рассмотрим прямоугольный треугольник ABC: ÐB = 90°, ÐA = a, BC = 2R. Найдем катет BA и гипотенузу AC: BA = BC × ctga, 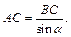 Так как в усеченный конус вписан шар, то образующая этого конуса равна сумме радиусов его оснований. Получим равенство:
Так как в усеченный конус вписан шар, то образующая этого конуса равна сумме радиусов его оснований. Получим равенство:
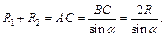
Заметим, что 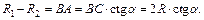
Решив систему 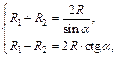 найдем
найдем
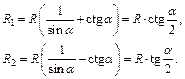
Вычисляем объем усеченного конуса по формуле (12.8).
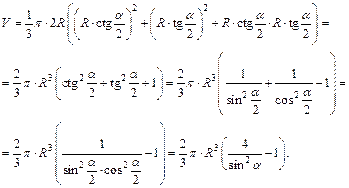
Получаем ответ: 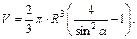
Пример 4. В шар радиуса R вписан конус, образующая которого составляет с плоскостью основания угол φ. Найти площадь полной поверхности конуса.
Решение. Для вычисления площади полной поверхности конуса необходимо знать радиус основания и образующую конуса. Рассмотрим осевое сечение данного конуса – равнобедренный треугольник SAB: SA = SB – образующие, SD – высота, DB – радиус основания конуса (рис. 12.51).
Рис. 12.51
По условию задачи ÐSAD = φ, следовательно, 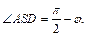 Треугольник AOS – равнобедренный (AO = OS = R), поэтому
Треугольник AOS – равнобедренный (AO = OS = R), поэтому 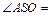
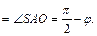 Внешний угол этого треугольника при вершине О равен: ÐAOD = ÐSAO + ÐASO = p – 2j.
Внешний угол этого треугольника при вершине О равен: ÐAOD = ÐSAO + ÐASO = p – 2j.
Из треугольника AOD (ÐD = 90°, AO = R, ÐAOD = p – 2j) выразим AD:
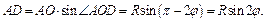
Из треугольника ASD (ÐD = 90°, AD = R sin 2j) выразим SA:
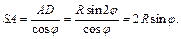
Подставив найденные выражения в формулу для вычисления площади полной поверхности конуса, получим:
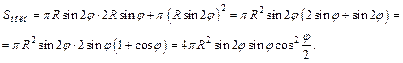
Таким образом, 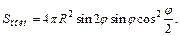
Пример 5. В прямой параллелепипед вписан цилиндр, объем которого в m раз меньше объема параллелепипеда. Найти двугранные углы при боковых ребрах параллелепипеда.
Решение. Двугранными углами при боковых ребрах данного параллелепипеда являются углы параллелограмма, лежащего в его основании. В параллелепипед вписан цилиндр, значит, в параллелограмм основания вписана окружность. Если в четырехугольник вписана окружность, то суммы длин противолежащих сторон четырехугольника равны. Таким образом, основанием параллелепипеда является ромб. Сделаем рисунок (рис. 12.52).

Рис. 12.52
Обозначим искомый угол a. Из треугольника ABC (ÐC = 90°, ÐA = a) найдем сторону ромба AB и его высоту BC:
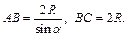
Так как высоты цилиндра и параллелепипеда равны, то площадь основания цилиндра будет в m раз меньше площади основания параллелепипеда. Запишем равенство: 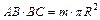 и выразим из него
и выразим из него 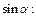
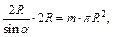 далее
далее 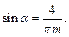
Двугранные углы при боковых ребрах параллелепипеда будут равны:
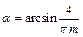 и
и 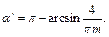
Дата добавления: 2015-09-29; просмотров: 2133;
