Примеры:________________________________________________________________________
1. Пусть события А и В несовместны и Р(А) ≠ 0, Р(В) ≠ 0. Значит, Р(А) .Р(В) ≠ 0. Найдем Р(А . В) = Р(?) = 0 . Поэтому Р(А . В) ≠ Р(А) .Р(В). Это означает, что несовместные события А и B зависимы.
2. Пусть событие А влечет за собой событие B, т.е. А Ì В, и Р(В) ≠ 1. Тогда А . В = А, и Р(А . В) = Р(А). Поэтому Р(А . В) ≠ Р(А) .Р(В). Это означает, что если А Ì В, то события А и В – зависимы.
________________________________________________________________
Формула полной вероятности и формула Байеса
Рассмотрим п попарно несовместных событий H1, H2, . . . , Hn. Они образуют полную группу событий, если они попарно несовместны, а их сумма является достоверным событием, т.е.
Hi . Нj = ? при i ≠ j и H1 +H2 + . . . + Нn = Ω.
Такие события называются гипотезами.
Простейшим примером полной группы событий является произвольное событие А и его дополнение Ā. По теореме сложения вероятностей, для полной группы событий справедливо равенство
Р(Н1) + Р(Н2) + . . .+ Р(Нп) =1.
Примеры:
__________________________ _____________________________
1. Пусть Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Рассмотрим события H1 = {2, 4, 6, 8, 10}, H2 = {1, 3}, H3 = {5, 7, 9}. Они попарно несовместны, а их сумма является достоверным событием Ω. Значит, Н1, H2, H3 составляют полную группу событий. Для них Р(Н1) = 5/10, Р(H2) = 2/10, Р(Н3) = 3/10, т.е. сумма их вероятностей равна 1.
2. В лесу растут деревья, среди которых 60 % берез, 10 % елей, и 30 % сосен. [3, c. 16]. Случайным образом выбирается для замера одно из деревьев. Обозначим гипотезы: Н1 – «выбранное дерево – береза», H2 – «выбранное дерево – ель», H3 – «выбранное дерево – сосна». Тогда события H1, H2, H3 – попарно несовместны, Р(Н1) = 0,6, Р(Н2) = 0,1, Р(Н3) = 0,3. Значит, гипотезы H1, H2, H3 составляют полную группу событий. Сумма их вероятностей равна 1.
_______________________________________________________________________________
Пусть события H1, H2, . . ., Нп образуют полную группу событий. Тогда для любого события А имеет место формула полной вероятности:
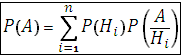
Пример:
_______________________________________________________________________
Рассмотрим предыдущий пример 2. Пусть при замере диаметра деревьев он оказался больше 15 см для 30 % берез, 40 % елей и 70 % сосен. Введем событие А – «диаметр случайно выбранного дерева больше 15 см». Найдем вероятность этого события. По условию примера, условные вероятности события А равны: Р(А/H1) = 0,3, P(А/H2) = 0,4, Р (А/H3) = 0,7. Тогда по формуле полной вероятности имеем:
Р(А) = P(H1)P (А/H1) + Р(Н2)Р(А/H2) + Р(Н3)Р(А/H3) = 0,6 . 0,3 + 0,1 . 0,4 + 0,3 . 0,7 = 0,43.
___________________________________________________________________
В формулу полной вероятности входят вероятности Р(Н1), Р(Н2), . . ., Р(Нn), которые называются априорными. Это вероятности гипотез Нi , вычисленные до опыта (a priori). Если событие А наступило, то эти вероятности изменяются. Это будут апостериорные условные вероятности, вычисленные после опыта (a posteriori) P(H1/A), PA(H2/A), . . . , PA(Hn/A). Они могут быть найдены по формуле Байеса:
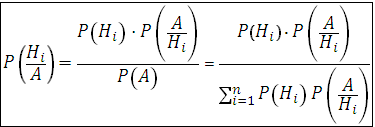
Дата добавления: 2015-09-28; просмотров: 958;
