Примеры:________________________________________________________________________. 1. Пусть производится выбор одного из чисел от 1 до 30

1. Пусть производится выбор одного из чисел от 1 до 30. Пусть событие В означает выбор четного числа, событие А – выбор числа, кратного 4. Тогда А Ì В, так как каждое число, кратное 4, является четным.

2. Пусть производится выбор одного из чисел от 1 до 30. Если событие В — выбор числа, кратного 5, а событие А — выбор числа, оканчивающегося цифрами 0 или 5, то А = В.

3. Пусть при выборе одного из чисел от 1 до 10 событие А озна­чает выбор четного числа. Значит, А = {2, 4, 6, 8, 10}, т.е. событие А состоит из элементарных событий — выборов одного из чисел 2, 4, 6, 8, 10. Собы­тие В — выбор числа, кратного 3. B ={3, 6, 9}, т.е. событие В состоит из элементарных событий — выборов одного из чисел 3, 6, 9. Тогда событие А + В означает выбор числа, кратного или 2, или 3 (при этом не исключается, что число кратно и 2 и 3), т.е. А + В = {2, 3, 4, 6, 8, 10}. состоит из элементарных событий — выборов одного из чисел Событие А ^. В означает выбор числа, кратного и 2 и 3 одновременно, т.е. А ^. В={6}.

______________________________________________________________

Операции над событиями можно представить как операции над множествами. При этом события представляются подмноже­ствами универсального множества Ω (достоверное событие). С помощью диаграммам Венна это изображено на рис. 5.1.

Ω Ω Ω

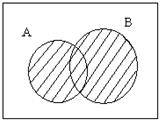
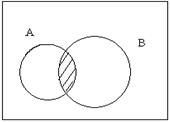
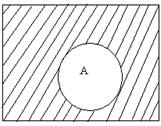
A B A B

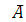
Рис. 5.1

Свойства операций над событиями:

1. =А.

2. А + В = В + А, А · В = В · А – коммутативность.

3. (А+В)+С=А+(В+С), (А·В)·С=А·(В·С) – ассоциативность.

4. А(В+С)=АВ+АС – дистрибутивность.

5. 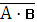= + , = 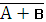· – аналог законов Де Моргана.

6. А+А=А, А · А = А.

7. А + ? = А, А · Ω =А.

8. А + Ω = Ω, А · ? = ?.

9. А · = ?,А + = Ω.