Пример 4. Броуновское движение

Частица радиусом r и массой m находится в жидкости с динамической вязкостью η при температуре Т и совершает броуновское движение. Докажем формулу Эйнштейна (1905 г.) для среднего квадрата смещения частицы за время t

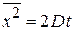, (П.1.25)

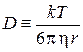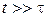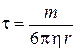где – диффузионная постоянная, и выполняется , где – время релаксации движения частицы под действием трения.

Смещение x частицы происходит с течением времени хаотически из-за ударов микрочастиц, совершающих тепловые движения. На частицу в жидкости действует сила вязкого трения, пропорциональная ее скорости

,

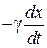где коэффициент трения

.

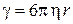Хаотически налетающие микрочастицы действуют с силой 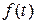. Из второго закона Ньютона для частицы массой m получаем уравнение

.

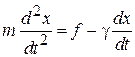Переходим к средним значениям. Для этого слагаемые умножаем на x

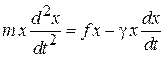
и используем равенства

,

.

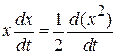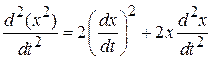Получаем уравнение

.

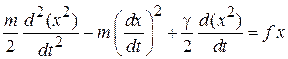Слагаемые усредняем по большому числу частиц. Учитываем

,

,

.

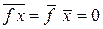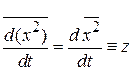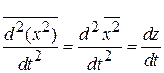Теорема о распределении тепловой энергии дает

.

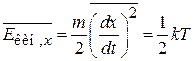Уравнение получает вид

,

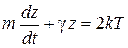или

,

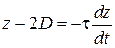где

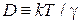– диффузионная постоянная;

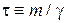– время релаксации под действием вязкого трения.

Разделяем переменные и интегрируем

,

,

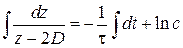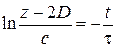находим

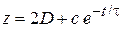. (П.1.26)

Второе слагаемое описывает процесс релаксации. Время релаксации

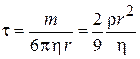
уменьшается при увеличении вязкости жидкости η, при уменьшении инертности шарика, его плотности ρ и радиуса r. Если время движения гораздо больше времени релаксации 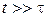, то пренебрегаем вторым слагаемым (П.1.26) и получаем

.

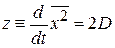Интегрирование дает формулу Эйнштейна (П.1.25)

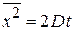
– средний квадрат смещения частицы за время t пропорционален времени.

Например, кварцевый шарик диаметром 1 мкм совершает броуновское движение в воде при комнатной температуре и проходит путь 1 нм за время 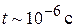. Его баллистическое движение происходит на пути ~ 1Å, время релаксации 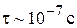. Выполняется 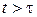и применима формула Эйнштейна.

Приведенный вывод формулы Эйнштейна предложил Поль Ланжевен в 1908 г. На основе (П.1.25) Жан Перрен измерил постоянную Больцмана в 1926 г. и получил число Авогадро. Существенное влияние на броуновское движение оказывает вихревое турбулентное течение жидкости, увлекаемой движением частицы. Этот эффект учли В. Владимирский и Ю.А. Терлецкий в 1945 г. Им можно пренебречь для движения частицы в газе.

При малом времени перемещения 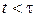сила трение не успевает существенно повлиять, частица движется баллистически и проходит путь 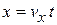, тогда

.

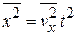Энергия движения определяется температурой

,

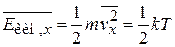откуда 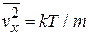. В результате средний квадрат смещения частицы пропорционален температуре и квадрату времени

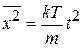. (П.1.27)

Броуновское движение, вызванное тепловой энергией, создает тепловой шум. Как следует из (П.1.25), при тепловом шуме среднее квадратичное смещения частицы пропорционально температуре и корню квадратному из времени смещения, если оно превышает время релаксации. Тепловое движение включает два этапа. На первом частица получает толчок от микрочастицы и движется баллистически, при этом система выведена из равновесного состояния. На втором этапе за счет трения восстанавливается равновесное состояние по истечении времени релаксации. Множество таких процессов образует тепловой шум. Тепловые флуктуации обеспечивают возвращение системы в равновесное состояние после любого воздействия на нее. При большом времени релаксации по сравнению со временем между столкновениями с микрочастицами релаксация не существенна, пренебрегаем ею, тогда тепловой шум становится импульсным процессом и превращается в дробовой шум. Тепловой шум возникает в объеме системы, где существенны процессы релаксации, дробовой шум в процессах транспорта между частями системы, где релаксация не существенна.

При подаче на резистор постоянного напряжения помимо теплового шума появляется 1/f-шум со спектральной плотностью, зависящей от частоты f по закону 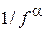, где параметр 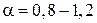варьирует для разных материалов. Закон 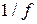выполняется в интервале частот 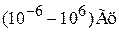, причем нижний предел экспериментально не достигнут. Этот шум наблюдается во всех материалах и устройствах электроники, а также в разнообразных явлениях природы. Его описал J.B. Johnson в 1925 г. Отсутствует понимание физических причин 1/f-шума и его общая теория. Возможно, он связан с флуктуациями сопротивления за счет числа носителей тока, или их подвижности. Возможен также вклад космических факторов в 1/f-шум.