Динамічне програмування
Динамічне програмування (динамічне планування) являє собою математичний метод оптимізацїї рішень, спеціально пристосований до так званих «багатоступеневих» (чи «багатоетапних») операцій. Багато економічних процесів дійсним чином діляться на ступені. До них можна віднести планування і управління виробництвом чи окремими процесами, розвиток яких відбувається із врахуванням часу, тобто в динаміці. Тимчасовим ступенем в них може бути період стратегічного планування, п'ятирічка, рік, місяць, день і навіть години. В інших операціях ділення на ступені приходиться вводити штучно: наприклад, процес виведення ракети на орбіту можна умовно поділити на етапи, кожен з яких займає якийсь часовий відрізок [22].
Процес в даному випадку керований, бо на кожному ступені приймається певне рішення, від якого залежить успіх даного кроку і операції в цілому.
Керування ніби складається із ряду елементарних, «ступеневих» керувань.
В економічній практиці зустрічаються завдання, які за постановкою і методами розв'язання відносяться до завдань динамічного програмування перспективного оптимального і поточного плануванням/розподілу тих чи інших ресурсів оптимізації ресурсів і вкладення їх у виробництво і т.п. Тут доцільно познайомитися з деякими завданнями, що розв'язуються методами динамічного програмування, викладені в загальному вигляді в роботі В.М. Колпакова [22].
1. Завдання перспективного планування
Планується діяльність промислового об'єднання, що складається з кількох підприємств, на період реалізації поставленої мети. Необхідно розподілити наявні ресурси, які в подальшому витратяться і одержиться прибуток. Періодично ресурси можуть перерозподілятися. Постає завдання розподілу ресурсів між підприємствами, що забезпечують максимальний прибуток всього об'єднання.
2. Завдання з оптимального керівництва поставками
В різних економічних, господарських ситуаціях з'являється завдання вибору часу (моменту подання) партії поставки і її об'єму, тобто, як прийнято називати, визначення оптимальної партійності деталей, конструкцій, сировини і матеріалів. З розміщенням замовлень пов'язані деякі фіксовані витрати, що не залежать від величини замовленої партії, а залежать тільки від факту замовлення. З утриманням матеріальних ресурсів пов'язані витрати, пропорціональні залишку нереалізованої продукції.
При розв'язанні цього завдання з багатьох можливих керувань вибирається таке, при якому досягається мінімум витрат на замовлення і утримання матеріальних ресурсів.
З наведених прикладів можна виділити типові особливості багатоступеневих завдань.
1. Розглядається система і її стан на кожному ступені без врахування того, яким шляхом вона прийшла в нього.
2. На кожному ступені вибирається одне рішення, під дією якого система переходить з попереднього стану в новий.
3. Дія на кожному ступені пов'язана з певним виграшем (прибутком) чи із втратою (витратами), залежними від стану на початок ступеня і прийнятого рішення.
4. На показники стану і управління можуть бути накладені обмеження, що визначають ділянку допустимих рішень.
5. В ході розв'язання знаходиться допустиме керування для кожного ступеня, що дозволяє одержати (екстремальне) значення функції мети через необхідну кількість ступенів. Послідовність дій персоналу керування, що на кожному ступені переводить систему з початкового стану в кінцевий, називають стратегією управління.
Динамічне програмування (планування) служить для вибору найкращого плану виконання багатоетапних дій. Для багатоетапних дій характерне протікання в часі. Крім дій, що дійсно носять багатоетапний характер (наприклад, перспективне планування), в ряді завдань звертаються до штучного розчленування на етапи, для того щоб зробити можливим застосування методу динамічного програмування.
В загальному вигляді постановка завдання динамічного програмування зводиться до наступного:
Є деяка керована операція (ціленаправлена дія), що розкладається (дійсно чи штучно) на т кроків — етапів. На кожному кроці здійснюється розподіл і перерозподіл учасників операції з метою покращення її результату в цілому. Ці розподіли в динамічному програмуванні називаються управлінням операцією і позначаються буквою V. Ефективність операції в цілому оцінюється тим же показником, що і ефективність її управління W(U).
При цьому ефективність управління W(U) залежить від всієї сукупності керувань на кожному кроці операції:
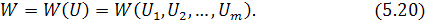
Управління, при якому показник W досягає максимуму, називається оптимальним управлінням. Оптимальне управління U є, як було сказано вище, багатоступеневим процесом і складається із сукупності оптимальних ступеневих керувань:

Завдання динамічного програмування полягає у визначенні оптимального управління на кожному ступені U (і =1, 2, ..., m) і, тим самим, досягається оптимальне керування всією операцією (процесом) в цілому.
В більшості практичних завдань приймається, що показник ефективності операції W в цілому являє собою суму ефективності дій на всіх етапах (ступенях) операції.
Інакше кажучи, в формалізованому вигляді процес можна
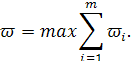
де ωi – ефективність операції на i-му ступені.
При цьому у випадку оптимального управління
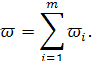
Суть розв'язання завдань динамічного програмування полягає в наступному:
· оптимізація проводиться методом послідовних наближень (ітерацій) в два круги; спочатку від останнього ступеня операції до першого, а потім, навпаки, — від першого до останнього ступеня;
· на першому крузі, йдучи від наступних ступенів до попередніх, знаходиться так зване умовне оптимальне управління; умовне оптимальне управління вибирається таким, щоб всі попередні ступені забезпечували максимальну ефективність наступного ступеня. Інакше кажучи, на кожному кроці наявне таке управління, яке забезпечує оптимальне продовження операції. Цей принцип вибору керування називається принципом оптимальності;
· так триває до першого кроку, але оскільки перший крок не має попереднього, то одержане для нього умовне оптимальне управління втрачає свій умовний характер і стає просто оптимальним управлінням, яке ми шукаємо;
· другий круг оптимізації починається з першого кроку, для якого оптимальне управління відоме.
Маючи для всіх кроків після нього умовні оптимальні управління, ми знаємо, що необхідно робити на кожному наступному кроці. Це дає нам можливість послідовно переходити від умовних до оптимальних управлінь для всіх наступних кроків, що забезпечує оптимальність операції в цілому.
Приклад завдання. Нехай маємо т типів різних вантажів, якими необхідно завантажити транспортний засіб (корабелі,, літак, автомобіль) таким чином, щоб загальна цінність вантажу IV була максимальною. Цінність вантажу є функцією від вантажопідйомності транспортного засобу:
s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:color w:val="000000"/><w:spacing w:val="1"/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>. (5.22)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Відома маса вантажів і-го типу Рі і її вартість Сі. Необхідно завантажити транспортний засіб таким чином, щоб загальна цінність вантажу була максимальною:
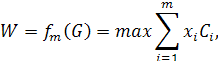
де хi — кількість предметів вантажу i-го типу, що завантажуються в транспортний засіб; хi виступає тут в ролі управління (Ui = хі). Обмежувальними умовами є:
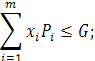
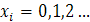
Перша умова вимагає, щоб загальна маса вантажу не перевищувала вантажопідйомність транспортного засобу, а друга умова (5.23) — щоб предмети, що складають вантаж різних типів, були неподільні.
Дата добавления: 2015-09-21; просмотров: 1340;
