Лінійне програмування
Успішність розв'язання переважної більшості економічних завдань залежить від найкращого, найвигіднішого способу використання ресурсів. В процесі економічної діяльності доводиться розподіляти такі важливі ресурси, як гроші, товари, сировину, обладнання, робочу силу та ін. І від того, як будуть розподілятися ці, як правило, обмежені ресурси, залежить кінцевий результат діяльності, бізнесу.
Суть методів оптимізацїї полягає в тому, що, виходячи з наявності певних ресурсів, вибирається такий спосіб їх використання (розподілу), при якому забезпечується максимум (чи мінімум) показника, що нас цікавить.
При цьому враховуються певні обмеження, що накладаються на використання ресурсів умовами економічної ситуації.
В якості методів оптимізацїї в економіці вважають використання всіх основних розділів математичного програмування (планування) лінійне, нелінійне і динамічне.
Як. було сказано раніше (див. 12.2 посібника), лінійне програмування є одним із вдалих методів використання ІСО.
Лінійне програмування (планування) — математичний метод відшукування максимуму чи мінімуму лінійної функції при наявності обмежень у вигляді лінійних нерівеностей чи рівнянь. (Лінійне тут означає, що на графіку функції зображуються у вигляді прямих ліній, що означають 1-ий ступінь відповідної величини).
Максимізуюча (мінімізуюча) функція являє собою прийнятий критерій ефективності розв'язання завдань, що відповідає Поставленій меті. Вона носить назву цільової функції.
Обмеження характеризують наявні можливості розв'язання завдання.
Суть розв'язання завдань лінійного програмування полягає в знаходженні умов, що спрямовують цільову функцію в мінімум чи максимум.
Рішення, що задовольняє умови завдання і відповідає поставленій меті, називається оптимальним планом.
Лінійне програмування (планування) служить для вибору найкращого плану розподілу обмежених однорідних ресурсів ч метою розв'язання поставлених завдань.
Якщо кількість змінних системи обмежень і цільової функції в математичній моделі завдання лінійного програмування дорівнює двом або трьом, то таке завдання можна розв'язані графічно чи аналітичне. При більшій кількості змінних завдання розв'язують, як правило, аналітичним шляхом.
В загальному вигляді постановка завдання лінійного програмування полягає в наступному. Умови завдання подаються з допомогою системи лінійних рівнянь чи нерівностей, що виражають обмеження, які накладаються на використання наявних ресурсів:

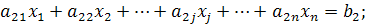
………………………………………………
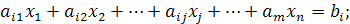
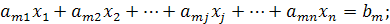
j = 1, 2, …, n; i = 1, 2, …, m; m < n; xj ≥ 0, (5.12)
де xj — шукані величини, що містять розв'язання поставленого завдання; аij і bi — відомі постійні величини, що характеризують умови завдання.
Цільова функція (лінійна форма) надається у вигляді:
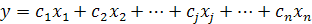
j = 1, 2, …, n, (5.13)
де сj — постійні коефіцієнти (коефіцієнти вартості).
Умови завдання (обмеження) можуть бути надані також у вигляді нерівностей. В таких випадках можна навести систему лінійних обмежень до вигляду (5.12), вводячи в кожне лінійне обмеження додаткові невід'ємні невідомі:
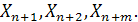 (5.14)
(5.14)
Цільова установка оптимізації полягає в тому, щоб звести очікувані при розв'язані даного завдання витрати підприємств до мінімуму.
Загальне математичне формулювання завдання відповідає умовам (5.12) і (5.13)
Перший рядок системи рівнянь (5.12)
 (5.15)
(5.15)
в даному прикладі це означає наступне:
а11 — кількість одиниць ресурсів вигляду 1 на першому підприємстві,
а12 — кількість одиниць ресурсів вигляду 1 на другому підприємстві і т.п,
b1 — загальний ресурс ресурсів вигляду 1 (для всіх підприємств);
х1, x2, т д. — шукана кількість підприємств типу 1,2 і т.д. Другий рядок згаданої системи рівнянь містить аналогічні величини для ресурсів вигляду 2 і т. д. Функція мети відповідає формулі (5.13). Треба повернути в мінімум величину
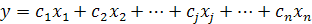 , (5.16)
, (5.16)
де с – показник, що характеризує витрати підприємств.
Нехай m — загальна кількість різних видів ресурсів, якими володіє власник, аn — кількість типів підприємств, між якими ці ресурси повинні бути розподілені. При цьому відомо, яка кількість однорідних ресурсів різного виду (і = 1,2... т) може бути реалізована на кожному з підприємств даного типу (j = 1, 2...п), а також загальна кількість ресурсів даного виду (b1). Відомо також відносне значення витрат на кожному з підприємств (сj).
Завдання полягає в тому, щоб найкращим (оптимальним) чином розподілити наявні ресурси за підприємствами, тобто знайти невідомі величини xj — потрібні для цієї кількості підприємств даного типу.
Геометрична інтерпретація завдання лінійного програмування можлива лише при наявності двох незалежних змінних. При трьох змінних наочне уявлення істотно ускладнюється, так як в цьому випадку має місце деякий випуклий багатогранник в трьох-вимірному просторі, що відповідає об'єму допустимих планів.
При кількості змінних більше трьох завдання втрачає геометричну наочність, так як важко уявити собі, наприклад, четирьохвимірний простір. Проте ідея одержання рішення, розглянутого вище, зберігає зміст і для випадку багатовимірного простору.
На основі такої ідеї створений і розроблений один з основних методів розв'язання завдань лінійного програмування — так званий симплекс-метод.
Симтекс-метод — алгебраїчна форма розв'язання завдання лінійного програмування, що випливає з тільки що розглянутого геометричного уявлення. При обґрунтуванні симплекс-методу будемо звертатися до вже розглянутого вище двохвимірного випадку, що дозволить досить просто перейти від геометричного уявлення до його алгебраїчної аналогії (див., наприклад, п. 8.4. [13]).
Дата добавления: 2015-09-21; просмотров: 765;
