Нелінійне програмування
Нелінійне програмування (планування) — математичні методи пошуку максимуму чи мінімуму функції при наявності обмежені, у вигляді нерівностей чи рівнянь.
Максимізуюча (мінімізуюча) функція являє собою прийнятий критерій ефективності розв'язування завдання, що відповідає поставленій меті. Він носить назву цільової функції.
Обмеження характеризують наявні можливості розв'язання завдання.
Цільова функція чи хоча б одне з обмежень нелінійні (тобто на графіках зображуються непрямими — кривими лініями).
Суть розв'язання завдань нелінійного програмування полягає в тому, щоб знайти умови, що перетворюють цільову функцію в мінімум чи максимум.
Рішення, що задовольняє умови завдання і відповідає поставленій меті, називається оптимальним планом.
Нелінійне програмування служить для вибору найкращого плану розподілу обмежених ресурсів з метою розв'язання поставленого завдання.
В загальному вигляді постановка завдання нелінійного програмування зводиться до наступного.
Умови завдання надаються з допомогою системи нелінійних рівнянь чи нерівностей, що виражають обмеження, накладені на використання наявних ресурсів:
Z1(x1, x2, …, xn) > 0;
Z2(x1, x2, …, xn) > 0;
Zm(x1, x2, …, xn) > 0; (5.17)
при хi > 0,
де Z1, Z2, …, Zm – відповідні функції, що характеризують умови розв'язання поставленого завдання (обмеження); хi — шукані величини, що містять розв'язання даного завдання.
Цільова функція подається у вигляді:
y = f(x1, x2, …, xn). (5.18)
Причому, в крайньому разі, одна із функцій у, Z1, Z2, …, Zm – нелінійна.
Методами нелінійного програмування розв'язуються завдання розподілу неоднорідних ресурсів.
Нехай маємо т різнорідних ресурсів, які передбачається реалізувати для бізнесу в п регіонах країни.
Відомі оціночні можливості (ймовірності) почати бізнес в j-му регіоні (Рj), а також ефективності використання i-го ресурсу в n-му регіоні (wij).
Розподіл ресурсів за регіонами характеризується так званим параметром управління (hij):
0, якщо і-й ресурс не направляється в j-й регіон,
hij=
1, якщо і-й ресурс направляється в j-й регіон.
Необхідно розподілити ресурси по регіонах таким чином (вибирати такі значення hij), щоб величина повної ймовірності досягнення мети Рц була максимальною:
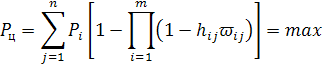
Повинно виконуватися також обмеження
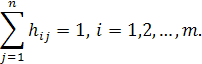
Це обмеження означає, що кожен із m ресурсів обов'язково повинен призначатися в який-небудь з регіонів.
В додатку 2 даного посібника наведені деякі типові завдання, що розв'язуються з допомогою методів нелінійного програмування, які ілюструють його можливості і прийоми розв'язання.
В цілому нелінійне програмування займається оптимізацією моделей завдань, в яких або обмеження, або показник ефективності (цільова функція), або те й інше — нелінійні. До методів нелінійної оптимізації можна віднести:
· аналітичні, що використовують методи диференційного
і варіаційного обчислення. Вони використовуються при
відсутності обмежень і при їх наявності типу рівності і
(чи) нерівності;
· чисельні;
· графічні, що базуються на графічному подаванні функцій, що підлягають максимізації чи мінімізації;
· методи дослідження можливих варіантів, засновані на
ідеї генерування можливих варіантів з метою вибору
найкращого з них;
· експериментальні (вони в даний час виділені в новий напрямок — математичну теорію планування експерименту) [22].
Приклад завдання.
При переїзді в нове місто з'являється необхідність доставки до нового місця проживання домашніх речей. При цьому відома ціна кожної речі, її вага і габарити.
Кількість і вид домашніх речей, які ми можемо відвезти, лімітуються вантажопідйомністю машини чи розмірами контейнера.
В ході розв'язання завдання зі всього набору предметів вибираються найбільш цінні (з максимальною сумарною вартістю предметів), вага яких вміщається у вантажопідйомність.
Завдання нелінійного програмування на практиці зустрічаються досить часто, наприклад, коли витрати ростуть непропорційно кількості закуплених чи вироблених товарів (ефект «оптовості»). Багато нелінійних завдань можуть бути приблизно замінені лінійними (лініаризовані), в крайньому випадку, в галузі, близькій до оптимального рішення.
Дата добавления: 2015-09-21; просмотров: 656;
