Теорема о параллельном переносе силы

Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить параллельно самой себе из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

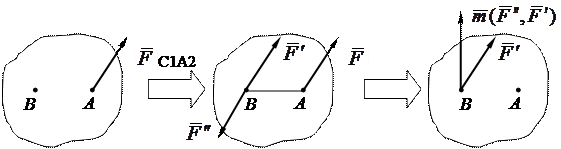Доказательство:

а) б) в)

Рис. 3.1

, ,

,

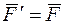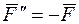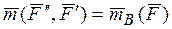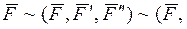пара ).

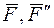Теорема о приведении системы сил к силе и паре:

Любую систему сил, приложенную к твердому телу, элементарными преобразованиями можно привести к одной силе, равной главному вектору 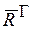системы сил и приложенной в произвольно выбранной точке О и к паре момент которой равен главному моменту 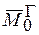данной системы сил относительно точки О.

Доказательство:

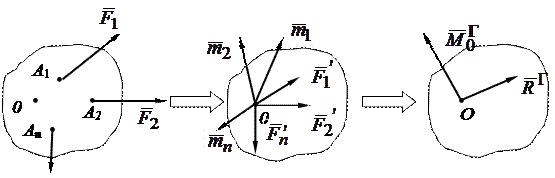
а) б) с)

Рис. 3.2

Пусть на твердое тело действует произвольная система сил 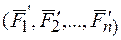,(рис.3.2 а)). Выберем какую-нибудь точку О за центр приведения и пользуясь теоремой Пуансо перенесем все силы в центр О, присоединения при этом соответствующие пары. Тогда на тело будут действовать система сил 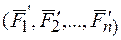, приложенная в точке О, и система пар, моменты которой 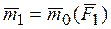, ,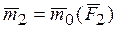…., . 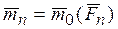Сходящие силы по аксиоме А3 заменим одной силой, которая по определению равна главному вектору (рис.3.2 с))

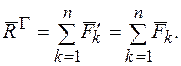
Чтобы сложить пары, нужно сложить моменты этих пар (рис. 3.2 с))

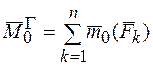- главный момент системы сил по определению.

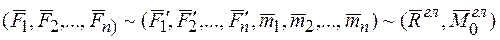(3.1)

Теорема доказана.

Замечание. Значение 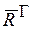от выбора центра О не зависит, значение же 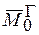при изменении центра О может в общем случае измениться.