Теорема сложения пар
Система, состоящая из нескольких пар 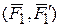 ,
, 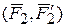 , …,
, …, 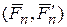 эквивалентна одной паре
эквивалентна одной паре 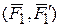 , момент которой равен геометрической сумме моментов заданных пар:
, момент которой равен геометрической сумме моментов заданных пар:
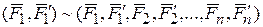 ,
,
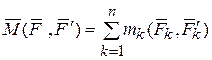 .
.
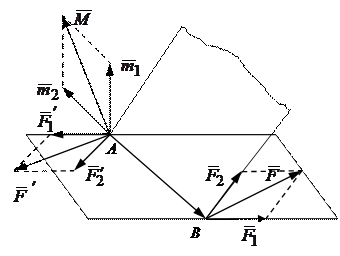 Докажем теорему для двух пар с моментами
Докажем теорему для двух пар с моментами 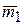 и
и 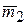 , лежащих в плоскостях I и II.
, лежащих в плоскостях I и II.
Рис.2.10
Возьмем на линии пересечения плоскостей отрезок АВ=d и изобразим пару с моментом 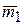 силами
силами 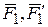 , а пару с моментом
, а пару с моментом 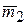 - силами
- силами 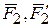 . Сложив силы в точках А и В, убеждаемся, что пары
. Сложив силы в точках А и В, убеждаемся, что пары 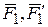 и
и 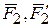 действительно эквивалентны одной паре
действительно эквивалентны одной паре 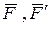 . Найдем момент этой пары. Так как
. Найдем момент этой пары. Так как 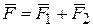 , то
, то 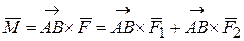 и следовательно
и следовательно 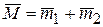 .
.
Последовательно применяя результат, полученный для двух пар, найдем, что данная система пар будет эквивалентна одной паре с моментом
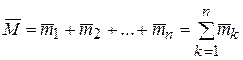 .
.
Дата добавления: 2015-09-21; просмотров: 733;
