Регрессия по методу наименьших квадратов.

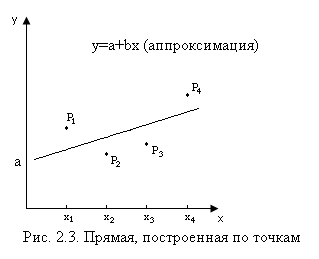
Допустим, что вы имеете четыре наблюдения для х и у, представленные на рис. 2., и перед вами поставлена задача — определить значения a и b в уравнении (2.1). В качестве грубой аппроксимации вы можете сделать это, отложив четыре точки Р и построив прямую, в наибольшей степени соответствующую этим точкам. Это сделано на рис.2.3 (слайд).

Отрезок, отсекаемый прямой на оси у, представляет собой оценку a и обозначен а, а угловой коэффициент прямой представляет собой оценку b и обозначен b.

С самого начала необходимо признать, что вы никогда не сможете рассчитать истинные значения a и b при попытке построить прямую и определить положение линии регрессии. Вы можете получить только оценки, и они могут быть хорошими или плохими. Иногда оценки могут быть абсолютно точными, но это возможно лишь в результате случайного совпадения, и даже в этом случае у вас не будет способа узнать, что оценки абсолютно точны.

Это справедливо и при использовании более совершенных методов. Построение линии регрессии на глаз является достаточно субъективным. Более того, как мы увидим в дальнейшем, это просто невозможно, если переменная у зависит не от одной, а от двух или более независимых переменных. Возникает вопрос: существует ли способ достаточно точной оценки a и b алгебраическим путем?

Первым шагом является определение остатка для каждого наблюдения. За исключением случаев чистого совпадения, построенная вами линия регрессии не пройдет точно ни через одну точку наблюдения. Например, на рис.4 (слайд 2.4) при х = x₁ соответствующей ему точкой на линии регрессии будет R₁ со значением у, которое мы обозначим 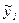вместо фактически наблюдаемого значения у₁. Величина 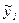описывается как расчетное значение у, соответствующее х₁ . Разность между фактическим и расчетным значениями (у₁ - 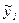)определяемая отрезком P₁R₁,, описывается как остаток в первом наблюдении. Обозначим его е₁. Соответственно, для других наблюдений остатки будут обозначены как е₂,, е₃ и е₄.

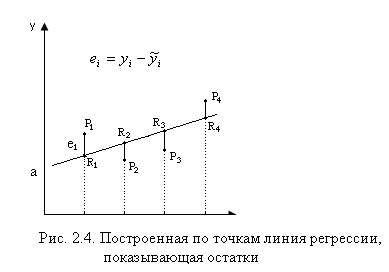
Очевидно, что мы хотим построить линию регрессии таким образом, чтобы эти остатки были минимальными. Очевидно также, что линия, строго соответствующая одним наблюдениям, не будет соответствовать другим, и наоборот. Необходимо выбрать такой критерий подбора, который будет одновременно учитывать величину всех остатков. Существует целый ряд возможных критериев, одни из которых «работают» лучше других. Например, бесполезно минимизировать сумму остатков. 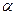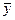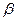Сумма будет автоматически равна нулю, если вы сделаете равным , а равным нулю, получив горизонтальную линию 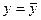. В этом случае положительные остатки точно уравновесят отрицательные, но строгой зависимости при этом не будет.

Один из способов решения поставленной проблемы состоит в минимизации суммы квадратов S. Для рис. 2.4 верно такое соотношение :

S = 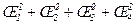(2.2)

Величина S будет зависеть от выбора а и b, так как они определяют положение линии регрессии. В соответствии с этим критерием, чем меньше S, тем строже соответствие. Если S=0, то получено абсолютно точное соответствие, так как это означает, что все остатки равны нулю. В этом случае линия регрессии будет проходить через все точки, однако, вообще говоря, это невозможно из-за наличия случайного члена.

Существуют и другие достаточно разумные решения, однако при выполнении определенных условий метод наименьших квадратов дает несмещенные и эффективные оценки a и b. По этой причине метод наименьших квадратов является наиболее популярным в вводном курсе регрессионного анализа.

После построения линии регрессии стоит более детально рассмотреть общее выражение для остатка в каждом наблюдении. Логика этого рассмотрения является достаточно простой. Однако на первый взгляд она может показаться абстрактной, поэтому более наглядно графическое представление.

На рис. 5 (слайд 2.5) линия регрессии

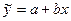(2.3)

построена по выборке наблюдений. Для того чтобы не загромождать график, показано только одно такое наблюдение: наблюдение i, представленное точкой Р c координатами (x_i,,y_i).

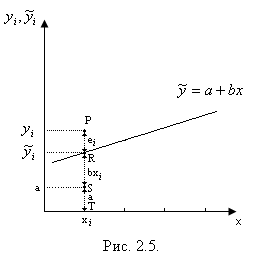
Когда х=х_i линия регрессии предсказывает значение у= 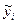что соответствует точке R на графике, где

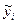= a + bx_i (2.4)

Используя условные обозначения, принятые на рис.5, это уравнение можно переписать следующим образом:

RT = ST + RS (2.5)

так как отрезок ST равен а, а отрезок RS равен bx_i

Остаток PR — это разность между РТ и RT:

PR = PT - RT = PT - ST - RS (2.6)

Используя обычную математическую запись, представим формулу (6) в следующем виде:

e_i = y_i - 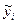= y_i - a - bx_i. (2.7)

Если бы в примере, показанном на графике (рис.5) мы выбрали несколько большее значение а или несколько большее значение b, то прямая прошла бы ближе к Р, и остаток e_i был бы меньше. Однако это повлияло бы на остатки всех других наблюдений, и это необходимо учитывать. Минимизируя сумму квадратов остатков, мы попытаемся найти некоторое равновесие между ними.

Рассмотрим случай, когда имеется п наблюдений двух переменных х и у. Предположив, что у зависит от х, мы хотим подобрать уравнение:

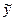= a + bx (2.8)

Расчетное значение зависимой переменной 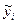и остаток e_i, для наблюдения i заданы уравнениями (2.4) и (2.7). Мы хотим выбрать а и b, чтобы минимизировать величину S, где S = åe_i².

Можно доказать, что величина S минимальна, когда

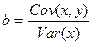(2.9)[1]

и 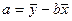(2.10)¹

Варианты выражения для b.

Так как

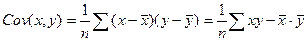(2.11)

и 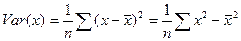(2.12)

мы можем получить следующие выражения для b:

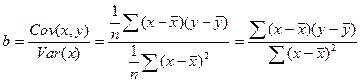(2.13)

b = 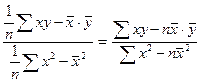(2.14)

В дальнейшем будет использоваться первоначальное определение b=Cov(х,y)/Var(х) и это выражение, вероятно, легче всего запомнить. На практике для вычисления коэффициентов регрессии используется компьютер, поэтому нет смысла запоминать альтернативные выражения. Зная определения выборочной дисперсии и ковариации, вы всегда сможете вывести эти выражения.