Модель парной линейной регрессии.

Коэффициент корреляции показывает, что две переменные связаны друг с другом, однако он не дает представления о том, каким образом они связаны. Рассмотрим более подробно те случаи, для которых мы предполагаем, что одна переменная зависит от другой.

Сразу же отметим, что не следует ожидать получения точного соотношения между какими-либо двумя экономическими показателями, за исключением тех случаев, когда оно существует по определению. В учебниках по экономической теории эта проблема обычно решается путем приведения соотношения, как если бы оно было точным, и предупреждения читателя о том, что это аппроксимация. В статистическом анализе, однако, факт неточности соотношения признается путем явного включения в него случайного фактора, описываемого случайным остаточным членом. Начнем с рассмотрения простейшей модели:

y=a +b x+u (2.1)

Величина у, рассматриваемая как зависимая переменная, состоит из двух составляющих: 1) неслучайной составляющей a + b x , где x выступает как объясняющая (или независимая) переменная, а постоянные величины a и b — как параметры уравнения; 2) случайного члена и.

На рис. 2.2 (слайд) показано, как комбинация этих двух составляющих определяет величину у. Показатели х_1, х₂, х₃, х₄ - это четыре гипотетических значения объясняющей переменной. Если бы соотношение между у и х было точным, то соответствующие значения у были бы представлены точками Q₁, Q₂, Q₃, Q₄ на прямой. Наличие случайного члена приводит к тому, что в действительности значение у получается другим. Предполагалось, что случайный член возмущения положителен в первом и четвертом наблюдениях и отрицателен в двух других. Поэтому если отметить на графике реальные значения у при соответствующих значениях х, то мы получим точки P₁, P₂, P₃, P₄ .

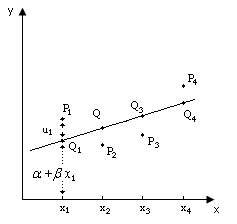
Рис. 2.2.

Следует подчеркнуть, что точки Р — это единственные точки, отражающие реальные значения переменных на рис. 2. Фактические значения a и b и, следовательно, положения точек Q неизвестны, так же как и фактические значения случайного члена. Задача регрессионного анализа состоит в получении оценок a и b и, следовательно, в определении положения прямой по точкам Р. Очевидно, что чем меньше значения и, тем легче эта задача. Действительно, если бы случайный член отсутствовал вовсе, то точки Р совпали бы с точками Q и точно показали бы положение прямой. В этом случае достаточно было бы просто построить эту прямую и определить значения a и b.

Почему же существует случайный член? Имеется несколько причин. 1. Невключение объясняющих переменных. Соотношение между у и х почти наверняка является очень большим упрощением. В действительности существуют другие факторы, влияющие на у, которые не учтены в формуле (2.1). Влияние этих факторов приводит к тому, что наблюдаемые точки лежат вне прямой. В результате мы получаем то, что обозначено как и. Если бы мы точно знали, какие переменные присутствуют здесь, и имели возможность точно их измерить, то могли бы включить их в уравнение и исключить соответствующий элемент из случайного члена..

2. Агрегирование переменных. Во многих случаях рассматриваемая зависимость — это попытка объединить вместе некоторое число микроэкономических соотношений. Например, функция суммарного потребления — это попытка общего выражения совокупности решений отдельных индивидов о расходах. Так как отдельные соотношения, вероятно, имеют разные параметры, любая попытка определить соотношение между совокупными расходами и доходом является лишь аппроксимацией. Наблюдаемое расхождение при этом приписывается наличию случайного члена.

3. Неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Здесь можно привести один из многих возможных примеров. Если зависимость относится к данным о временном ряде, то значение у может зависеть не от фактического значения х, а от значения, которое ожидалось в предыдущем периоде. Если ожидаемое и фактическое значения тесно связаны, то будет казаться, что между у и х существует зависимость, но это будет лишь аппроксимация. Расхождение вновь будет связано с наличием случайного члена.

4. Неправильная функциональная спецификация. Функциональное соотношение между у и х математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Безусловно, надо постараться избежать возникновения этой проблемы, используя подходящую математическую формулу, но любая самая изощренная формула является лишь приближением, и существующее расхождение вносит вклад в остаточный член.

5. Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить вклад в остаточный член.

Остаточный член является суммарным проявлением всех этих факторов. Очевидно, что если бы нас интересовало только измерение влияния х на у, то было бы значительно удобнее, если бы остаточного члена не было. Если бы он отсутствовал, мы бы знали, что любое изменение у от наблюдения к наблюдению вызвано изменением х, и смогли бы точно вычислить b. Однако в действительности каждое изменение у отчасти вызвано изменением и, и это значительно усложняет жизнь.