Интерпретация уравнения регрессии.

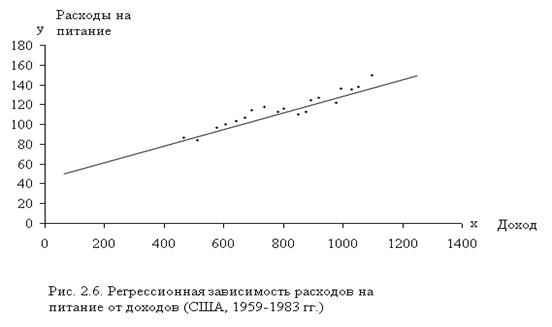
Интерпретации уравнения регрессии состоит в словесном истолковании уравнения так, чтобы это было понятно человеку, не являющемуся специалистом в области статистики. Проиллюстрируем это моделью регрессии для функции спроса, т. е. регрессией между расходами потребителя на питание (у) и располагаемым личным доходом (x) по данным для США за период с 1959 по 1983 г. Данные представлены в виде графика (рис.2.6).

Предположим, что истинная модель описывается следующим выражением:

у = a + bх + и (2.15)

и оценена регрессия

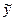= 55,3 + 0,093х . (2.16)

Полученный результат можно истолковать следующим образом. Коэффициент при х (коэффициент наклона) показывает, что если х увеличивается на одну единицу, то у возрастает на 0,093 единицы. Как х, так и у измеряются в миллиардах долларов в постоянных ценах; таким образом, коэффициент наклона показывает, что если доход увеличивается на 1 млрд. долл., то расходы на питание возрастают на 93 млн. долл. Другими словами, из каждого дополнительного доллара дохода 9,3 цента будут израсходованы на питание.

Что можно сказать о постоянной в уравнении, равной 55,3? Формально говоря, она показывает прогнозируемый уровень у, когда х = 0. Иногда это имеет ясный смысл, иногда нет. Если х = 0 находится достаточно далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам; даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантии, что так же будет при экстраполяции влево или вправо (рис.2.6).

В рассматриваемом случае экстраполяция к вертикальной оси приводит к выводу о том, что если доход был бы равен нулю, то расходы на питание составили бы 55,3 млрд. долл. Такое толкование может быть правдоподобным в отношении отдельного человека, так как он может израсходовать на питание накопленные или одолженные средства. Однако оно не имеет никакого смысла применительно к совокупности. В данном случае константа выполняет единственную функцию: она позволяет определить положение линии регрессии на графике. Можно привести пример постоянной, которая имеет ясный смысл. По этим же данным (приложение 1) можно определить регрессионную зависимость расходов на питание у от времени, определенного как t = 1 для 1959 г., t =2 для 1960 г. и т.д. Она задана уравнением:

= 95,3 + 2,53 t. (2.17)

В этом уравнении постоянную 95,3 можно объяснить как расходы на питание при t = 0 для 1958 г.

При интерпретации уравнения регрессии чрезвычайно важно помнить о трех вещах. Во-первых, а является лишь оценкой a, а b — оценкой b. Поэтому вся интерпретация в действительности представляет собой лишь оценку. Во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. В-третьих, верность интерпретации зависит от правильности спецификации уравнения.

В сущности, мы построили довольно наивную зависимость для функции спроса. Мы будем неоднократно возвращаться к этому в следующих разделах, уточняя как определение, так и статистические методы, используемые для оценки коэффициентов уравнения.

Подводя итог сказанному, можно представить интерпретацию линейного уравнения регрессии в виде реализации следующих шагов.

Во-первых, можно сказать, что увеличение х на одну единицу (в единицах измерения переменной х) приведет к увеличению значения у на b единиц (в единицах измерения переменной y). Вторым шагом является проверка, каковы действительно единицы измерения х и у, и замена слова «единица» фактическим количеством. Третьим шагом является проверка возможности более простого выражения результата, который может оказаться не вполне удобным. В примере, приведенном в данном разделе, в качестве единицы измерения для х и у использовались миллиарды долларов, что позволило произвести очевидные упрощения.

Постоянная а дает прогнозируемое значение y (в единицах y), если х= 0. Это может иметь или не иметь ясного смысла в зависимости от конкретной ситуации.

2.5 Качество оценки: коэффициент R².

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной у. В любой данной выборке у оказывается сравнительно низким в одних наблюдениях и сравнительно высоким — в других. Мы хотим знать, почему это так. Разброс значений у в любой выборке можно суммарно описать с помощью выборочной дисперсии Var (у).

В парном регрессионном анализе мы пытаемся объяснить поведение у путем определения регрессионной зависимости у от выбранной независимой переменной х. После построения уравнения регрессии мы можем разбить значение у_i в каждом наблюдении на две составляющих — и е_i.

y_i = 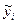+ e_i (2.18)

Величина 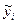— расчетное значение у в наблюдении i — это то значение, которое имел бы у при условии, что уравнение регрессии было правильным, и отсутствии случайного фактора. Это, иными словами, величина у, спрогнозированная по значению x в данном наблюдении. Остаток e_i есть расхождение между фактическим и спрогнозированным значениями величины y. Это та часть у, которую мы не можем объяснить с помощью уравнения регрессии. Используя уравнение (2.18), разложим дисперсию у:

Var (y) = Var ( 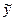+ e ) = Var ( 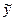) + Var(e) + 2Cov ( 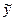,e) (2.19)

Далее, Cov ( 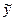,е) должна быть равна нулю. Следовательно, мы получаем:

Var (y) = Var ( 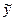) + Var (e) (2.20)

Это означает, что мы можем разложить Var (у) на две части: Var ( 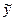) — часть, которая «объясняется» уравнением регрессии в вышеописанном смысле, и Var (е) — «необъясненную» часть.

Согласно (2.20), Var ( 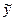)/ Var (у) — это часть дисперсии y, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают R ².

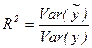(2.21)

что равносильно

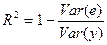(2.22)

Слова «объясненный» и «необъясненный» взяты в кавычки, так как объяснение, в сущности, может быть мнимым. В действительности у может зависеть от какой-то другой переменной z, и х может действовать как величина, замещающая z . Поэтому вместо слова «объясненный» здесь лучше употреблять выражение «представляющийся объясненным».

Максимальное значение коэффициента детерминации равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что 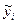= у_i для всех i и все остатки равны нулю. Тогда Var ( 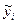) = Var (у), Var (е) = О и R² = 1.

Если в выборке отсутствует видимая связь между у и х, то коэффициент R² будет близок к нулю.

При прочих равных условиях желательно, чтобы коэффициент R² был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов а и b, чтобы максимизировать R². Не противоречит ли это нашему критерию, в соответствии с которым а и b должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков? Нет, легко показать, что эти критерии эквивалентны, если (2.22) используется как определение коэффициента R². Отметим сначала, что

e_i = y_i - 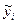= y_i - a -bx_i (2.23)

откуда, беря среднее значение е_i по выборке и используя уравнение (2.10), получим:

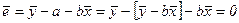(2.24)

Следовательно,

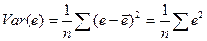(2.25) Отсюда следует, что принцип минимизации суммы квадратов остатков эквивалентен минимизации дисперсии остатков при условии выполнения (2.10). Однако если мы минимизируем Var(e), то при этом в соответствии с (2.22) автоматически максимизируется коэффициент R.².

Альтернативное представление коэффициента R²

На интуитивном уровне представляется очевидным, что чем больше соответствие, обеспечиваемое уравнением регрессии, тем больше должен быть коэффициент корреляции для фактических и прогнозных значений y, и наоборот. Покажем, что R² фактически равен квадрату такого коэффициента корреляции между у и 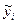, который мы обозначим 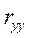(заметим, что Cov (е, у) = 0.

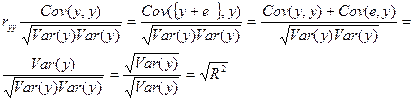(2.26)

[1] - доказательство формул (2.9) и (2.10) требует знания основ дифференциального исчисления и здесь не приводится, поэтому принимаем формулы расчета коэффициентов регрессии на веру.