Показательный закон распределения времени обслуживания

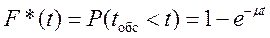
Плотность распределения:

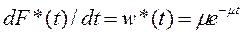
Рис. 5.9. Функция распределения и плотность распределения времени обслуживания для показательного закона

Среднее время обслуживания равно:

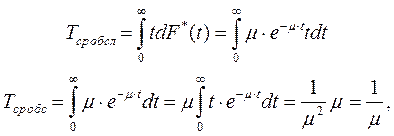
где μ – средняя скорость обслуживания;

μt – число заявок за время обслуживания t.

Д о с т о и н с т в а и с п о л ь з о в а н и я э к с п о н е н ц и а л ь н о г о

з а к о н а р а с п р е д е л е н и я

1) Вероятность, что время обслуживания закончится в малом интервале dt, не зависит от длительности предыдущего интервала обслуживания (система без памяти).

2) При прерывании обслуживания через время Т, оставшееся время (t–T) также распределено по экспоненциальному закону с тем же параметром μ.