Физические основы пластической деформации

В основе ОМД лежит процесс пластической деформации, при которой изменяется форма без изменения массы, либо объема (V=const).

Закон наименьшего сопротивления в теории ОМД гласит: при изменении формы тела каждая точка его перемещается в направлении наименьшего сопротивления.

Основное уравнение закона постоянства объема имеет вид

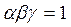(1)

где g - коэффициент деформации по высоте g = h₁ /h₀ b - коэффициент деформации по ширине b =b₁ /b₀

l - коэффициент деформации по длине l = l₁ /l_0.

Первоначальный объем V₀ = l₀ b₀ h₀, a деформированный объем V₁ = l₁ b₁ h₁

т.к. V₀ =V₁ , то l₀ b₀ h₀ = l₁ b₁ h₁ Þ l₁ /l₀*b₁/ b₀ * h₁/ h₀ = 1 Þ g b l = 1.

При прокатке b₁» b₀ (уширениeм можно пренебречь), тогда 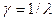и

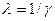
Скорость деформации и смещенный объем.

Прологарифмируем выражение (1):

Смысл (1) и (2) заключается в том, что уменьшение высоты вызывает увеличение по ширине и длине.

Натуральный логарифм коэффициента деформации в каком-либо направлении представляет собой _ удельный смещенный объем V_д/V в этом направлении, а сумма таких удельных объемов по всем направлениям равна нулю.

(3)

( e = l) - величина относительной деформации.

в) Краткие сведения из теории пластической деформации твер­дых тел.

При любом виде нагружения в материале возникают - нормальные (s_п)

и - касательные (s_t) напряжения:

s_n = s₀ cos² a , (4)

s_t = 0,5 s₀ sin2 a .

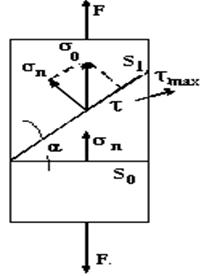
Рис. 18.6. Определение нормальных и касательных напряжений

В сечении S⁰ (при a = 0) возникают максимальные нормальные напряжения s_{n max} = s = F/S₀, а касательные s_t = 0.

Максимальное касательное напря­жение t s_{t max} = 0,5 при a =45°.

Плоскости, по которым касатель­ные напряжения не действуют, называ­ются главными плоскостями, а нор­мальные напряжения, действующие по главным плоскостям, называются глав­ными напряжениями.

Здесь рассмотрен простой случай растяжения в осевом направ­лении. Однако на практике материал подвергается растяжению или сжатию по двум, трем направлениям, т е находится в сложном на­пряженном состоянии.

В теории упругости показано, что в каждой точке любого на­пряженного тела (рис. 18.7) можно провести три взаимно перпендикулярные главные плоскости, через которые передаются три главных нормаль­ных напряжения s₁ ³ s₂ ³ s_3.

В каждой точке напряженного тела можно выделить элемен­тарный кубик, гранями которого служат главные плоскости, по кото­рым действуют три взаимно перпендикулярных главных напряжения. Если материал подвергается одному простому растяжению (или сжа­тию), то тело находится в линейно - напряженном состоянии, если двум - в плоско - напряженном состоянии, если трем взаимно перпендикулярным деформациям - то в объемно - напряженном состоянии.

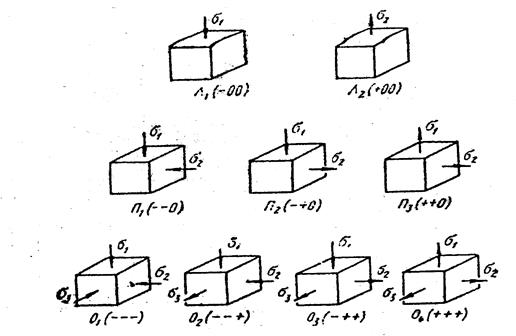Рис. 18.7. Возможные схемы деформации по С.И.Губкину

На рис. 18.7 приведены девять возможных схем напряжения и три основные схемы деформации. С помощью таких схем определяется пластичность металла. Так как число схем деформаций три, а напряжений девять, то одна и та же схема деформаций может быть осуществлена при различных схемах напряженного состояния. Приме­ром схемы Д_I служит прокатка узкой полосы, а широкой полосы проходит по схеме Д_II. По схеме Д_III протягивается металл через отверстие.

Сопротивление деформации зависит также от температуры и скорости деформации.

Теория предельного состояния устанавливает зависимость между пределом текучести и напряжениями в материале при его пла­стической деформации. В случае простого линейного растяжения (или сжатия) пластическая деформация начинается при s₁ = s_тех.

При сложном напряженном состоянии от s₂ ¹ 0; s₃ ¹ 0 вопрос о величине напряжений, возникающих при пластической деформации, может быть разрешен лишь с помощью теории предельного состояния. Согласно одной из теорий, пластическая деформация наступает, ко­гда разность s₁ - s₃ = s_тех, т.е. выполняется условие пластической деформации.

Однако эта теория не учитывает напряжения s₂. Наиболее раз­вита теория Губера. Мизесс и Генки - которая называется энергети­ческой.

Согласно этой теории - пластическая деформация в теле насту­пает, когда потенциальная энергия упругой деформации, направлен­ной на изменение формы тела, а не объема, достигает определенного значения.

Потенциальная энергия упругой деформации W_n = W₀ + W_F, где W₀, W_F - энергии, необходимые для изменения объема и формы.

При объемной деформации полная потенциальная энергия

W_n = (s₁ e₁ + s₂ e₂ + s₃ e₃)/2 (5)

(т.к. W_n = Ee²/2; s =E*e; W_n = (Ee)e/2 = s e/2).

По закону Гука

e₁ = [s₁ - m ( s₂ + s₃ )]/ Е (6)

e₂ = [s₂ - m ( s₁ + s₃ )]/ Е (7)

e₃ = [s₃ - m ( s₁ + s₂ )]/ Е (8)

Подставив (6)-(8) в (5), получим

W_n = [s₁² + s₂² + s₃² -2m( s₁s₂ + s₂s₃ + s₁s₃ )]/ (2Е) (9)

Воспользуемся тем обстоятельством, что приращение объема V_деф/V при упругой деформации равно сумме деформаций в трех вза­имно перпендикулярных направлениях, т.е.

D V/V = e₁ + e₂ + e₃ = 1 - 2m ( s₁ + s₂ + s₃ )/Е (10)

Объемная составляющая W₀ потенциальной энергии равна

W₀ = 0,5( DV/V)*( s₁ + s₂ + s₃ )/3 (11)

С учетом (10)

W₀ = ( s₁ + s₂ + s₃ )² (1 - 2m )/6Е (12)

Удельная потенциальная энергия W_F, направленная на изме­нение формы тела:

W_F = W_n - W₀ = [(s₁ - s₂ )² + (s₂ - s₃ )² + (s₃ - s₁ )² ](1 + 2m )/6Е (13)

При линейной деформации ( s₂ » 0; s₃ » 0; s₁ = s_Т )

W_флин = 2s_Т² (1 + m) / 6Е (14)

И следовательно, уравнение пластичности

(15)

В предельном случае при s₂ = s₃ ( либоs₂ = s₁ ) получим

s₁ - s₃ = s_тек (16)

что совпадает с условием пластичности (в неэнергетической теории).

Если же s₂ = (s₁ + s₃)/2 , получим

s₁ - s₃ = 1,15s_тек (17)

В общем случае, условие пластичности можно выразить уравнением

s₁ - s₃ = b s_тек (18)

где b = 1,0-1,15.

Уравнение пластичности (18) имеет большое значение при определении усилий, требующихся для ОМД.