Система електроприводу з модальним регулятором та самонастроювальним пристроєм корекції
Головною особливістю сучасної теорії керування є опис динамічних систем на основі поняття простору станів. Будь-яка система, яка описується кінцевим числом диференційних та алгебраїчних рівнянь, може бути подана у формі змінних стану
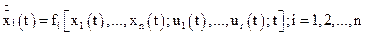 , (3.7)
, (3.7)
де 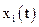 - змінні, які характеризують систему;
- змінні, які характеризують систему; 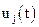 - вхідні дії;
- вхідні дії; 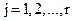 .
.
Змінні 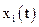 -це змінні простору станів. Знаючи їх сукупність у початковий момент часу та закон зміни
-це змінні простору станів. Знаючи їх сукупність у початковий момент часу та закон зміни 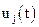 на інтервалі
на інтервалі 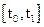 , можна визначити значення
, можна визначити значення 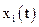 для будь-яких точок даного інтервалу часу.
для будь-яких точок даного інтервалу часу.
Вихідні змінні системи 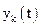 можуть бути виражені через
можуть бути виражені через 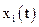 та
та 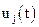
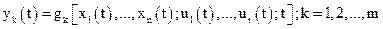 . (3.8)
. (3.8)
Використання методу простору станів у загальному випадку дозволяє виділити так звані керовану та некеровану, спостережену та неспостережену частини системи.
Математичний опис динамічної системи (3.7) та (3.8) схематично може бути подано (рис.3.15,а) у вигляді “чорного ящика” з вхідними 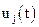 , вихідними
, вихідними 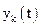 змінними, а також проміжними змінними
змінними, а також проміжними змінними 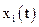 , які характеризують внутрішній стан.
, які характеризують внутрішній стан.
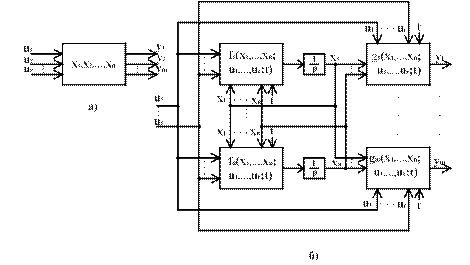 Рис.3.15. Спрощена та розгорнута структурні схеми системи
Рис.3.15. Спрощена та розгорнута структурні схеми системи
Застосування проміжних координат як змінних стану необхідно для усунення неоднозначності між керуючими діями та вихідними координатами системи. Розгорнута структурна схема, яка відповідає рівнянням (3.7), (3.8), наведена на рис.3.15,б. Більш компактно рівняння стану (3.7), (3.8) та відповідна структурна схема можуть бути подані у векторно-матричній формі. Сукупність вхідних змінних можна подати у вигляді 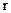 - мірного вектора вхідних дій або вектора керування
- мірного вектора вхідних дій або вектора керування
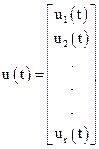 . (3.9)
. (3.9)
Сукупність вихідних змінних подамо у вигляді 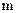 - мірного вектора виходу або вектора спостереження
- мірного вектора виходу або вектора спостереження
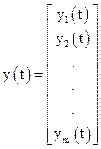 . (3.10)
. (3.10)
Сукупність координат, які характеризують внутрішній стан системи, подамо у вигляді 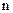 - мірного вектора стану
- мірного вектора стану
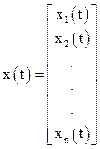 . (3.11)
. (3.11)
Сукупність нелінійних залежностей може бути подана вектор-функціями
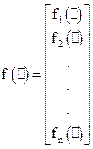 ;
; 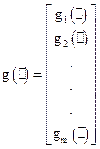 . (3.12)
. (3.12)
На підставі виразів (3.9)…(3.12) рівняння стану та виходу будуть мати вигляд
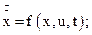
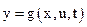 . (3.13)
. (3.13)
Відповідна рівнянням (3.13) структурна схема (рис.3.16) містить векторні величини, які подані подвійними стрілками.
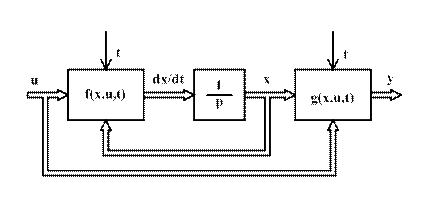
Рис.3.16. Структурна схема системи у векторно-матричній формі
Для лінійних систем рівняння (3.7) та (3.8) приймають вигляд
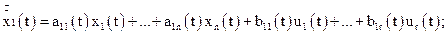 …………………………………………………………………......
…………………………………………………………………......
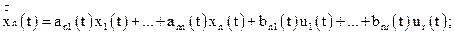 ……………………………………………………………………..
……………………………………………………………………..
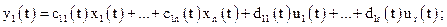 ……………………………………………………………………..
……………………………………………………………………..
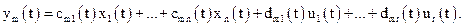 У векторно-матричній формі система буде мати вигляд
У векторно-матричній формі система буде мати вигляд
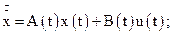
(3.14)
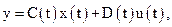
де 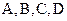 - матриці.
- матриці.
Матриця системи 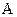 характеризує її динамічні властивості та є квадратною матрицею
характеризує її динамічні властивості та є квадратною матрицею 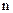 - го порядку
- го порядку
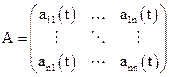 . (3.15)
. (3.15)
Матриця керування 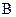 характеризує дію вхідних змінних на змінні стану та є прямокутною
характеризує дію вхідних змінних на змінні стану та є прямокутною 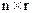 матрицею
матрицею
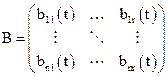 . (3.16)
. (3.16)
Матриця вимірювання 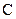 характеризує зв`язок вихідних координат зі змінними стану та має розмір
характеризує зв`язок вихідних координат зі змінними стану та має розмір 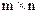
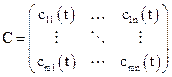 . (3.17)
. (3.17)
Матриця 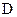 характеризує безпосередню дію входів на виходи та має розмір
характеризує безпосередню дію входів на виходи та має розмір 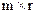
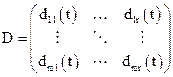 . (3.18)
. (3.18)
Для стаціонарної системи елементи цих матриць не залежать від часу, тому рівняння в змінних стану приймають вигляд
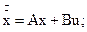
(3.19)
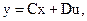
а відповідна для них векторно-матрична структурна схема наведена на рис.3.17.
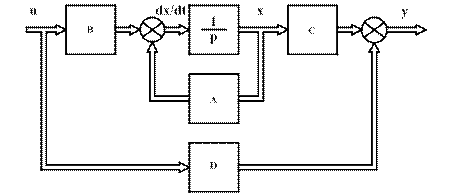
Рис.3.17. Векторно-матрична структурна схема системи
Поняття простору станів, керованості та спостережуваності важливі при створенні реальних систем, заснованих на принципі модального керування. Коли керуюча дія на впливає на змінну стану, то систему вважають некерованою. У разі коли система має властивість, яка дозволяє за майбутніми значеннями вихідної змінної визначити її стан у минулому, то систему називають спостережуваною.
Для того, щоб лінійна система була асимптотично стійкою, її полюси ( корені характеристичного рівняння) мають бути розташованими у лівій півплощині площина комплексних чисел. Бажане розташування полюсів на комплексній площині впливає на характер перехідних процесів в системі та може бути досягнуто за допомогою лінійного зворотного зв`язку за станом, що забезпечується модальним регулятором. Рівняння лінійного зворотного зв`язку за станом буде мати вигляд
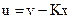 , (3.20)
, (3.20)
де 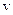 - вектор вхідних дій;
- вектор вхідних дій; 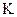 - матриця коефіцієнтів зворотних зв`язків.
- матриця коефіцієнтів зворотних зв`язків.
Підставляючи (3.20) у перше рівняння системи (3.19), дістанемо рівняння системи зі зворотним зв`язком за станом
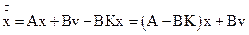 . (3.21)
. (3.21)
Векторно-матрична структурна схема, яка відповідає рівнянню (3.21), містить вихідну систему – об`єкт (рис.3.18) та модальний регулятор у колі зворотного зв`язку.
Динамічні властивості отриманої замкненої системи визначаються новою матрицею системи
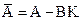 .
.
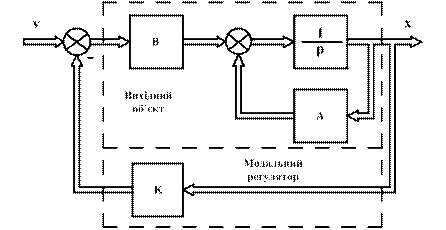
Рис.3.18. Векторно-матрична структурна схема системи з модальним регулятором
Завдання модального регулятора полягає у тому, щоб за допомогою матриці коефіцієнтів зворотних зв`язків система, яка замкнена зворотним зв`язком за станом, мала бажаний розподіл полюсів, що визначається бажаним характеристичним поліномом 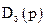
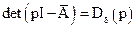 ,
,
де 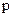 - оператор Лапласа;
- оператор Лапласа; 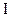 - одинична матриця розмірності
- одинична матриця розмірності 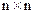 .
.
У якості бажаного характеристичного полінома використовують відомі стандартні форми, наприклад, поліноми Батерворта ( табл. 3.1).
Для визначення керованості системи (3.19) необхідно, щоб матриця керованості
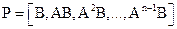
мала ранг, рівний порядку системи
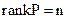 .
.
Таблиця 3.1
| Порядок полінома | Поліном Батерворта |
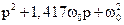
| |
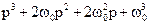
| |
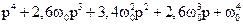
|
В якості прикладу визначимо керованість об`єкта, матриці якого
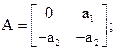
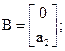
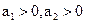 ,
,
число входів 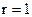 , а бажаний характеристичний поліном має вигляд
, а бажаний характеристичний поліном має вигляд
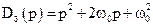 ,
,
де 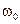 - константа, яка характеризує швидкодію системи.
- константа, яка характеризує швидкодію системи.
Знайдемо матрицю керованості
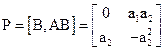 .
.
Досліджуваний об`єкт по входу повністю керований, оскільки 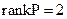 дорівнює порядку системи
дорівнює порядку системи 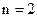 , а визначник
, а визначник 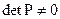 .
.
В якості іншого прикладу синтезуємо модальний регулятор для електроприводу постійного струму, якір двигуна якого підключений до вентильного перетворювача, а структурна схема у змінних стану наведена на рис.3.19. В якості змінних стану вибрано 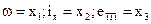 .
.
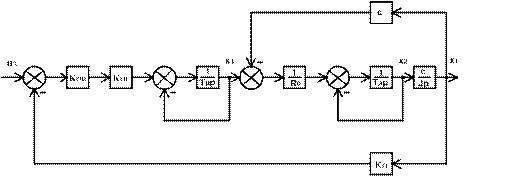
Рис.3.19. Структурна схема електроприводу постійного струму з вентильним перетворювачем
Система описується такою системою рівнянь
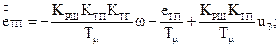
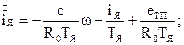 (3.22)
(3.22)
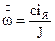 ,
,
де 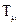 - сума малих некомпенсованих сталих часу.
- сума малих некомпенсованих сталих часу.
Позначимо вектор стану системи
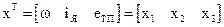 .
.
Система рівнянь (3.22) у векторно-матричній формі
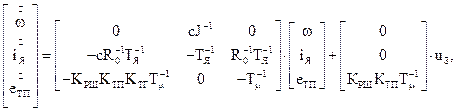
звідки рівняння станів
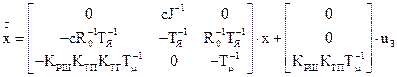 . (3.23)
. (3.23)
Для спрощення розімкнемо зворотний зв`язок за швидкістю та визначимо 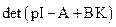 з врахуванням (3.23)
з врахуванням (3.23)

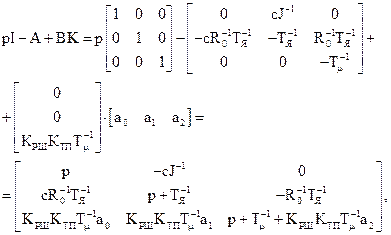
де 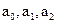 - коефіцієнти додаткових зворотних зв`язків за змінними стану
- коефіцієнти додаткових зворотних зв`язків за змінними стану 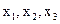 . Остаточно
. Остаточно
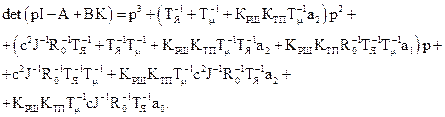 Прирівнюючи коефіцієнти при однакових степенях
Прирівнюючи коефіцієнти при однакових степенях 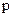 цього виразу та поліному Батерворта третього порядку із табл.3.1, одержимо коефіцієнти модального регулятора
цього виразу та поліному Батерворта третього порядку із табл.3.1, одержимо коефіцієнти модального регулятора
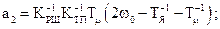
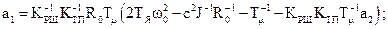
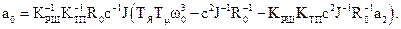
Модальний регулятор - це операційний підсилювач, до входу якого (рис.3.20) підключені з розрахованими коефіцієнтами відповідні давачі.
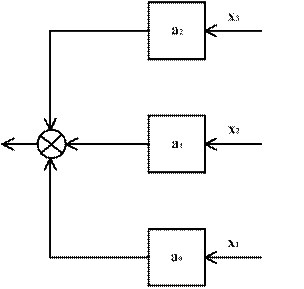
Рис.3.20. Схема модального регулятора
Розглянемо застосування модального регулятора для системи стабілізації потужності різання (рис.3.21) з електроприводом подачі типу ЕШІР1. Електропривод характеризується діапазоном регулювання швидкості 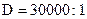 при коефіцієнті використання електродвигуна за струмом не гірше 0,99. Система побудована за принципом підпорядкованого керування з ПІ- регулятором швидкості та П- регулятором струму.
при коефіцієнті використання електродвигуна за струмом не гірше 0,99. Система побудована за принципом підпорядкованого керування з ПІ- регулятором швидкості та П- регулятором струму.
Контур швидкості в цьому випадку - це типова коливальна ланка зі сталою часу 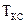 та відносним коефіцієнтом затухання
та відносним коефіцієнтом затухання 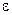 .
.

Рис.3.21. Система стабілізації потужності різання
металорізального верстату
Для системи стабілізації потужності різання розподіл коренів характеристичного полінома за стандартною формою Батерворта забезпечується у разі 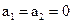 та коли
та коли
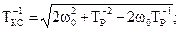
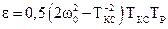 ,
,
де 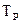 - стала часу процесу різання.
- стала часу процесу різання.
Коефіцієнт зворотного зв`язку за потужністю різання 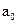 розраховується за умови забезпечення одиничного коефіцієнта передачі контуру стабілізації
розраховується за умови забезпечення одиничного коефіцієнта передачі контуру стабілізації
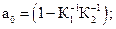
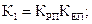
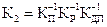 ,
,
де 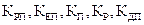 - відповідно коефіцієнти передачі
- відповідно коефіцієнти передачі
регулятора потужності, електроприводу, механізму подачі, процесу різання та давача потужності.
На рис.3.22 наведені графіки перехідних процесів системи стабілізації потужності різання у разі стрибкоподібної зміни коефіцієнта процесу різання.

Рис.3.22. Графіки перехідних процесів системи стабілізації потужності різання
Розглядувана система не забезпечує потрібний рівень стабілізації потужності різання у разі зміни 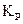 . Для підвищення якості роботи системи необхідно застосувати самонастроювальний пристрій корекції (рис.3.23).
. Для підвищення якості роботи системи необхідно застосувати самонастроювальний пристрій корекції (рис.3.23).
Рис.3.23. Структурна схема системи з самонастроювальним пристроєм корекції
Стійкість роботи, висока динамічна та статична точність роботи системи забезпечуються за рахунок самонастроювання коефіцієнта передачі 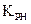 статичної моделі об`єкта керування залежно від зміни коефіцієнта
статичної моделі об`єкта керування залежно від зміни коефіцієнта 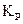 .
.
Нехай 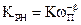 , де
, де 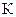 - постійне число;
- постійне число; 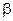 - деякий показник. Сигнал на виході статичної моделі об`єкта керування, яка є частиною пристрою корекції, дорівнює
- деякий показник. Сигнал на виході статичної моделі об`єкта керування, яка є частиною пристрою корекції, дорівнює
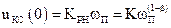 .
.
Сигнал на виході самонастроювального пристрою корекції дорівнює
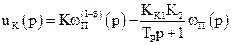 ,
,
де 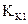 - коефіцієнт пропорційності.
- коефіцієнт пропорційності.
Графіки перехідного процесу системи при наявності самонастроювального пристрою корекції при зміні 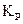 наведені на рис.3.24.
наведені на рис.3.24.

Рис.3.24. Графіки перехідного процесу системи при наявності самонастроювального пристрою корекції
При зміні 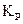 потужність різання встановлюється на заданому рівні, а кутова швидкість електроприводу подачі змінюється. При малій зміні
потужність різання встановлюється на заданому рівні, а кутова швидкість електроприводу подачі змінюється. При малій зміні 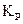 технологічний зворотний зв`язок розімкнений й кутова швидкість електроприводу подачі відповідає величині напруги завдання
технологічний зворотний зв`язок розімкнений й кутова швидкість електроприводу подачі відповідає величині напруги завдання 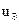 .
.
Використання модального регулятора для системи стабілізації потужності різання забезпечує потрібний рівень стабілізації тільки при стаціонарних параметрах контуру стабілізації. При значних змінах 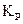 модальний регулятор має бути доповнений самонастроювальним пристроєм корекції, який дозволяє стабілізувати потужність різання
модальний регулятор має бути доповнений самонастроювальним пристроєм корекції, який дозволяє стабілізувати потужність різання 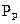 з похибкою не більше ніж 5% при значних змінах
з похибкою не більше ніж 5% при значних змінах 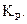
Дата добавления: 2015-09-18; просмотров: 1084;
