Примеры решения задач. Пример 2.1 Температура поверхностей вертикальной стенки высотой 3 м равна 10°С

Пример 2.1 Температура поверхностей вертикальной стенки высотой 3 м равна 10°С. Температура воздуха в помещении 20°С. Определить коэффициент теплоотдачи от воздуха к стенке.

Решение. Определяем значение критериев Gr и Pr

Gr=bgl³Dt/g²; Pr=g/a.

По таблице А1 приложения А по средней температуре t_cp=0,5(t_c+t_в)=15°С определяем параметры воздуха g, l и Pr.

g_ж=14,61×10^-6 м²/с; Pr_ж=0,705; l_ж=2,56×10^-2 Вт/(м×К).

;

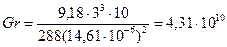Gr×Pr=4,31×10¹⁰×0,705=3,03×10¹⁰

Режим движения воздуха турбулентный, так как Gr×Pr>10⁹.

По формуле (2.2) подставляя вместо С и т их значения при вертикальной поверхности находим число Нуссельта

Nu=0,15(Gr×Pr)^0,33(Pr_ж/Pr_c)^0,25=0,15(3,03×10¹⁰)^0,33×1=431,48;

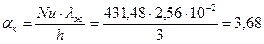Вт/(м²×К).

По приближенной формуле (2.3) для вертикальной поверхности

a_к 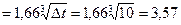Вт/(м²×К).

Пример 2.2. Определить теплопотери через окно с двойным остеклением размерами 1,2х1,4 м², если расстояние между стеклами 120 мм, температура поверхности стекол 18°С и -15°С.

Решение. Вычисляем эквивалентный коэффициент теплопроводности по формуле lэкв=l×eк, где l - действительный коэффициент теплопроводности воздуха, определяется по средней температуре воздуха по таблице А1 приложения А; eк – коэффициент конвекции, являющийся функцией Gr×Pr, который может приближенно вычислен по формуле eк=0,18(Gr×Pr)0,25. 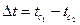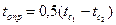За определяющий размер принимаем расстояние между стеклами d, за расчетную разность температур , за определяющую температуру ; tопр =0,5(18-15)=1,5°С. По таблице А1 приложения А определяем параметры воздуха gж=13,41×10-6 м2/с; lж=24,6×10-3 Вт/(м×К); Pr=0,71;

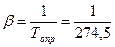К^-1.

Вычисляем произведение

.

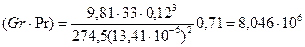Коэффициент конвекции e_к=0,18(8,046×10⁶)^0,25=9,58

Тогда

l_экв=9,58×24,6×10^-3=2,36×10^-1 Вт/(м×К).

Теплопотери через окно с двойным остеклением будут равны

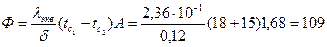Вт

Пример 2.3 Определить силу тока для нихромовой проволоки диаметром 1,0 мм из условия, что ее температура не будет превышать 300°С. сопротивление 1 погонного метра проволки при температуре 300°С R=6,0 Ом, температура окружающей среды t_m=20°C.

Расчет произвести для двух случаев.

- проволока находится в спокойном воздухе;

- проволока находится в спокойной воде под давлением при температуре насыщения выше 300°С.

Решение. По закону Ньютона-Рихмана определим мощность теплового потока от проволки к окружающей среде

q_l=pd_нa(t_c-t_ж).

Для определения a находим число Грасгофа и число Нуссельта:

а) окружающая среда воздух.

По таблице А1 приложения А находим физические параметры воздуха при t_опр=0,5(300+20)=160°С.

l_ж=3,64×10^-2 Вт/(м×К); g_ж=30,09×10^-6 м²/с; Pr_ж=0,682.

Число Грасгофа

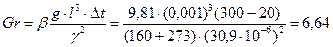
Gr×Pr=6,64×0,682=4,53.

По таблице 2.1 при произведении Gr×Pr=4,778

C=7,18; т=0,125, тогда по формуле (2.2)

Nu=1,18(Gr×Pr)^0,125=1,18×4,53^0,125=1,435.

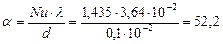Вт/(м²×К).

q_l=pd_н×a(t_c-t_ж)=3,14×0,001×52,2(300-20)=45,89 Вт/ч

q_e=J²R 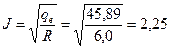А

Пример 2.4 В баке с раствором хлористого кальция размещен горизонтальный охлаждающий змеевик из труб, наружный диаметр которых 57 мм. Плотность раствора хлористого кальция при температуре 15°С r_ж=1220 кг/м³. Температура замерзания раствора t₃= -25,7°C, средняя температура наружной поверхности трубы t_ст=-20°С, температура раствора вдали от поверхности трубы t_ж=-10°С.

Определить коэффициент теплообмена a от раствора к поверхности трубы при свободном движении жидкости.

Решение. Теплоотдачу при свободном движении около горизонтальной трубы (змеевика) определяем по уравнению

Nu=0,5(Gr×Pr)^0,25.

Определяющим размером является наружный диаметр трубы, в качестве определяющей температуры принимаем среднюю температуру

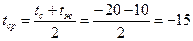°С.

Данная формула справедлива 1×10³£(Gr×Pr)£10³.

Определяем теплофизические свойства хлористого кальция при r=1220 кг/м³ и t₃=-25,7°C l_-20=0,523 Вт/(м×К)

l_-15=0,518 Вт/(м×К)

l_-20=0,511 Вт/(м×К)

g_-10=4,87×10 м²/с; g_-15=6,20×10 м²/с; g=7,77×10 м²/с;

Pr_-10=33; Pr_-15=42,5; Pr_-20=53,80;

b_-10=3,5×10^-4; b_-20=3,3×10^-4К¹; b_-15=3,4×10^-4К¹

Определяем критерии подобия, характеризующие процесс теплообмена:

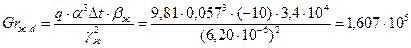
Ra=(Gr_d×Pr_ж)=(1,607×10⁵×42,5)=6829750=6,83×10⁶.

Nu_ж.d=0,5(6,83×10⁶)^0,25=25,56

Коэффициент теплообмена 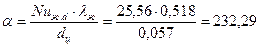Вт/(м²×К).