Теплоотдача суспензий
Во многих отраслях промышленности и сельского хозяйства приходится нагревать или охлаждать жидкостные суспензии мелкодисперсного порошка твердого тела в жидкости.
Согласно экспериментам проводимым в МВТУ им. Н.Э. Баумана Кафановым В.И. критериальное уравнение теплообмена при течении жидкостных суспензий в трубах имеет вид
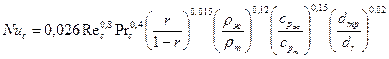 , (2,32)
, (2,32)
где Nuс – критерий Нуссельта суспензии;
Rec – критерий Рейнольдса суспензии;
Prc – критерий Прандтля суспензии;
r – объемная доля порошка твердого тела в суспензии
rж – плотность жидкости, кг/м3;
rт - плотность твердого тела, кг/м3;
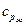 и
и 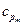 - теплоемкости жидкости и твердого тела, кДж/(кг×К);
- теплоемкости жидкости и твердого тела, кДж/(кг×К);
dтр и dr – диаметр трубы и средней диаметр частиц порошка твердого тела.
В качестве определяющей температуры принимают среднюю температуру среды tср=(t1+t2)/2, где t1 – температура среды на входе в теплообменник, а t2 – на выходе из него, °С.
Коэффициент гидравлического сопротивления x определяют по формуле:
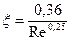 . (2.33)
. (2.33)
Теплопроводность суспензии lс определяют по формуле Максвелла
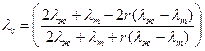 , (2.34)
, (2.34)
где lж – теплопроводность жидкости, Вт/(м×К);
lт – теплопроводность твердого тела, Вт/(м×К).
Динамическая вязкость суспензии mс определяют по формуле Вэнда
mс=mж(1+2,5r+7,17r2+16,2r3), (2.35)
где mж – динамическая вязкость жидкости, Па×с.
Выше перечисленными зависимостями можно пользоваться до 25% концентрации по объему.
Пример 2.12 По трубопроводу диаметром 50 мм и длиной 4 м протекает суспензия порошка меди в воде со скоростью w=1 м/с. Объемная концентрация меди 10%, средний диаметр частиц порошка 100×10-6 м. Определить количество теплоты передаваемой суспензии за 1 час, если температура жидкости 50°С, а температура стенки 70°С, а также коэффициент теплообмена a.
Решение. Подсчитываем отдельные множители, входящие в управление (2.32). Теплофизические параметры берем из приложения А таблица А5 и таблица Б1 приложения Б.
rс=rтr+rж(i+r)=8930×0,1+988,1(1+0,1)=1769,29 кг/м3
По формуле (2.35) определяем динамическую вязкость суспензии
mс=mж(1+2,5r+7,17r2+16,2r3)=543,4×10-6(1+2,5×0,1+7,17×(0,1)2+16,2(0,1)3=735×10-6 Н×с/м2=735×10-6 Па×с.
По формуле (2.34) находим lс суспензии

По формуле 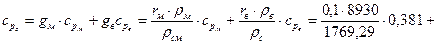
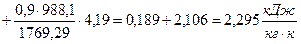
вычисляем теплоемкость суспензии.
Находим число Рейнольдса 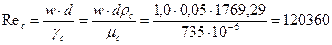 .
.
Число Прандтля 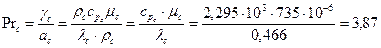
Число Нуссельта
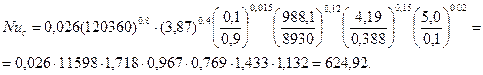
Находим коэффициент теплообмена aс
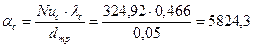 Вт/(м2×К)
Вт/(м2×К)
По закону Ньютона-Рихмана
Ф=aс×А(tс-tж)=5824×3,14×0,05×4×20=73149 Вт
Дата добавления: 2015-09-18; просмотров: 2138;
