Свободная (естественная) конвенция
Расчет коэффициента теплообмена при свободном движении теплоносителя в большом объеме обычно ведут по критериальному уравнению вида
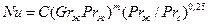(2.2)
где С и т – коэффициенты, зависящие от условий теплообмена.
Для газов можно считать Рr=const, а (Prж/Рrc)=1, и поэтому все приведенные формулы упрощаются.
При вычислении чисел подобия физические параметры g, l, a выбираются по средней температуре теплоносителя в объеме и у стенки:
tср=0,5(tж+tc).
Коэффициент объемного расширения газа b определяется по формуле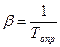 
или выбираются по приложениям для данного теплоносителя.
Среднее значение коэффициента теплообмена при естественной конвекции вертикальной поверхности можно получить из формулы (2.3)
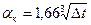, (2.3)
где Dt=tж-tc – перепад температур между температурой воздуха помещения и температурой поверхности стенки, °С.
Для определения среднего значения aк при горизонтальном расположении поверхности, если греющая поверхность расположена внизу (рисунок 1 б) или холодная поверхность – вверху, можно пользоваться формулой
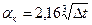. (2.4)
Таблица 2.1 Значения коэффициентов С и т
| Условия теплообмена | С | т | Определяющий размер |
| Вертикальные поверхности (трубы, пластины) 103<Gr×Pr<109 (ламинарный режим) | 0,76 | 0,25 | длина трубы, высота пластины |
| Gr×Pr>109 (турбулентный режим) | 0,15 | 0,33 | длина трубы, высота пластины |
| Горизонтальная труба 103<Gr×Pr<108 | 0,50 | 0,25 | диаметр трубы |
| Для тел любой формы О=(Gr×Pr)ср<10-3 | 0,50 | Для труб и шара диаметр, а для плит - высота | |
| 10-3<(Gr×Pr)ср<5×102 | 1,18 | 0,125 | |
| 5×102<(Gr×Pr)ср<2×107 | 0,54 | 0,25 | |
| 2×107<(Gr×Pr)ср<5×1013 | 0,135 | 0,33 | |
| Горизонтальная пластина при ламинарном режиме движения охлаждение сверху | 0,54 | 0,25 | короткая сторона пластины |
| охлаждение снизу | 0,27 | 0,25 |
Если греющая поверхность расположена вверху (рисунок 1 в) или холодная поверхность – внизу
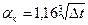. (2.5)
Расчет теплообмена в ограниченном объеме ведут по уравнениям теплопроводности, применяя эквивалентную теплопроводность
lэкв=l×eк, (2.6)
где eк – коэффициент конвекции, который определяется в зависимости от произведения Gr×Pr
Gr×Pr<103 er=1;
103<Gr×Pr<106 er=0,105(Gr×Pr)0,3; (2.7)
106<Gr×Pr<1010 er=0,40(Gr×Pr)0,2. (2.8)
В приложенных расчетах вместо (2.7) и (2.8) для всей области значений аргументов Gr×Pr>103 можно применить зависимость
eк=0,18(Gr×Pr)0,25, (2.9)
Дата добавления: 2015-09-18; просмотров: 1923;