Сжатие - растяжение по двум перпендикулярным направлениям (разноименная схема).

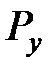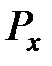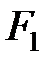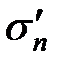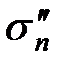Очевидно, что при сжатии - растяжении по двум перпендикулярным направлениям, Рисунок 13, силы и будут создавать на наклонной площадке нормальное напряжение , и направленные в разные стороны, и касательные напряжения 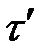и 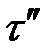, направленные в одну сторону.

Рисунок 13 Схемы напряжений при сжатии и растяжении по двум перпендикулярным направлениям.

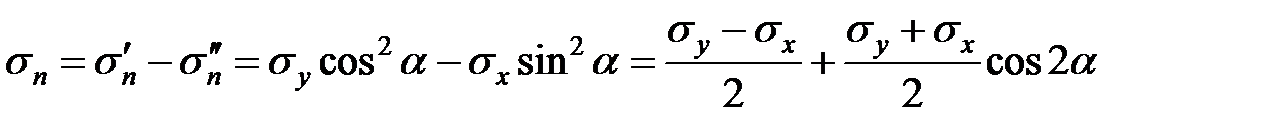
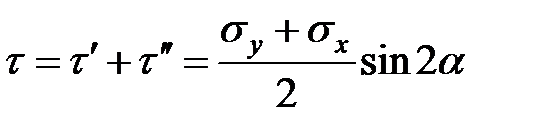
Напряжения 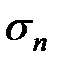и 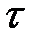, на круге Мора, характеризуются точкой В. При 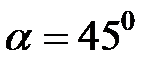получим:

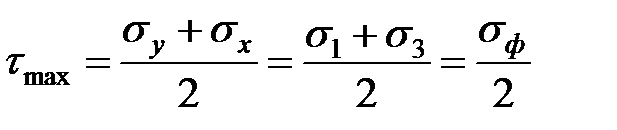
Отсюда следует, что при разноименной схеме деформации, сжатие-растяжение, максимальное касательное напряжение 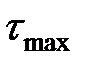равно полусумме абсолютных значений главных нормальных напряжений или фактическому сопротивлению деформации металла:

.

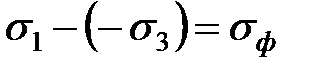Сравнивания одноименную и разноименную схему деформации предположим, что горизонтальное напряжение 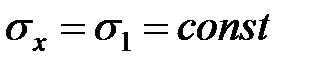. Далее следует, что для начальной стадии пластической деформации и для создания определенного касательного напряжения

,

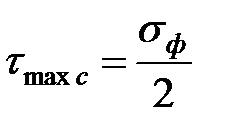нужно, в случае одноименной схемы, создать вертикальное напряжение 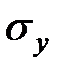равное:

.

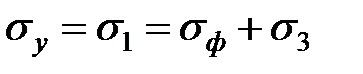В случае разноименной схемы:

.

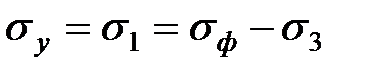Из формул видно, что в первом случае, одноименной схемы, вертикальное напряжение 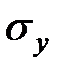больше чем во втором случае.

Из выше изложенного можно сделать вывод, что разноименная схема выгоднее, чем одноименная, так как при этой схеме выгоднее проводить деформацию металла. Пластическая обработка проходит при меньших вертикальных давления на металл со стороны рабочего инструмента, например валков прокатной клети или штампа. Это можно использовать, например, при прокатке с натяжением.

Рассматривая частный случай разноименной схемы, когда 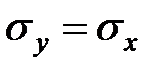и 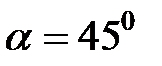. Из формул приведенных выше, а точнее:

,

,

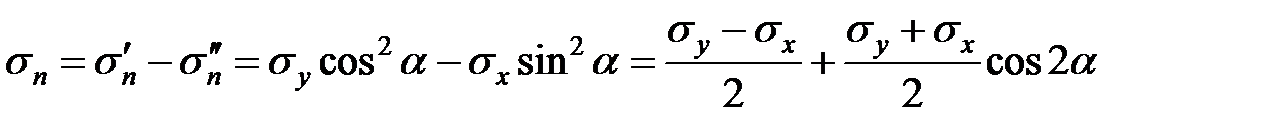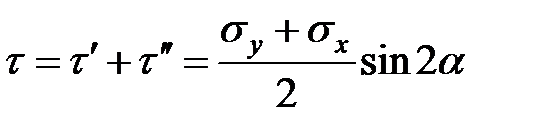Следует, что нормальное напряжение 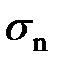, на наклонной площадке, будет равна нулю. При этом касательное напряжение 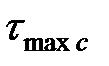будет, по прежнему, максимальным:

.

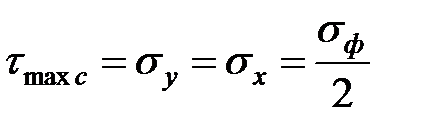Этот случай называется чистым сдвигом при пластической деформации.

Рассматривая одноименную и разноименную схемы деформации, которые можно назвать плоскими схемами, а сама деформация плоской или двухмерной. Так как в теории максимальных касательных напряжений учитываются напряжения в двух направлениях, по 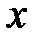оси и оси 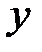. При этом напряжения по третьей оси 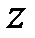, являющаяся перпендикуляром к плоскости 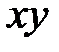, приравнивается нулю.