Краткая теория. При вращательном движении твердого тела вокруг неподвижной оси каждая точка тела движется в плоскости

При вращательном движении твердого тела вокруг неподвижной оси каждая точка тела движется в плоскости, перпендикулярной оси, по окружности, центр которой лежит на оси. Линейная скорость точки тела v связана с угловой скоростью тела.

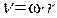, (1)

где r – расстояние от точки тела до оси вращения.

Кинетическая энергия тела равна сумме кинетических энергий всех частиц тела:

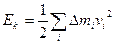, (2)

где 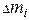- элементарные массы, на которые мысленно разбито тело. Подставляя скорость v_i из формулы (1) в (2), получим

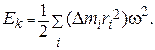(3)

Величина 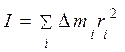(4)

называется моментом инерции тела. Момент инерции характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела.

Выражение для кинетической энергии вращающегося тела вокруг неподвижной оси, исходя из формул (3) и (4), выглядит следующим образом:

.

Для вычисления моментов инерции различных тел массу 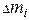в формуле (4) выражают через плотность тела: 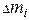= ρ ΔV_i , где ΔV_i – элементарный объем тела, и переходят к пределу ΔVi → 0. Тогда получим

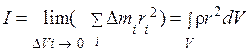. (6)

Теорема Штейнера устанавливает связь между моментом инерции тела I_с относительно оси, проходящей через центр инерции, и моментом инерции I этого тела относительно другой оси, параллельной первой .

,

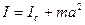где m – масса тела, а – расстояние между осями.

В настоящей работе измеряется момент инерции различных тел с помощью крутильного маятника. Этот маятник состоит из горизонтально расположенного поворотного стола, на котором могут закрепляться различные тела. На оси поворотного стола закреплен шкив радиусом R, с помощью которого столу может сообщаться вращательное движение. Через шкив перекинута нить, к концам которой прикреплены две пружины (рис. 1) c коэффициентами жесткости k₁ и k₂.

Рис. 1. Крутильный маятник

В положении равновесия силы натяжения нити по разные стороны от шкива одинаковы и равны упругим силам, которые согласно закону Гука

(F_упр)₀ = k₁ x₀₁ = k₂ x₀₂ , (8)

где x₀₁ и x₀₂ - величины растяжения пружин.

При отклонении от положения равновесия поворотный стол совершает колебания под действием сил упругости двух пружин. Величина деформации одной пружины x₁ = x₀₁ + х , где х – отклонение от равновесного положения. Если нить нерастяжимая, то величина деформации другой пружины

х₂ = х₀₂ – х.

Запишем выражение для потенциальной энергии деформации пружин следующим образом:

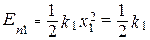(x₀₁ + x)² (9)

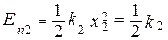( x₀₂ - x)² (10)

Если пренебрегать силами трения, то согласно закону сохранения механической энергии, полная механическая энергия, т. е. сумма кинетических и потенциальных энергий,

(x₀₁ + x)² + 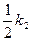(x₀₂ - x)² (11)

не зависит от времени. Значит, .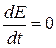

Вычисляя производную от выражения (11) по времени, получим

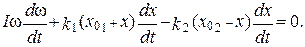(12)

Если нить не проскальзывает по шкиву поворотного стола, то

х = Rj ,

где j - угол поворота стола от положения равновесия; 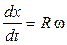. Учитывая условие равновесия (8) и определение угловой скорости 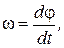получим из уравнения (12)

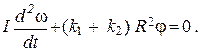(13)

Обозначим 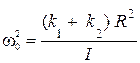и

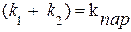– суммарный коэффициент жесткости двух пружин. Тогда уравнение (13) принимает вид дифференциального уравнения гармонических колебаний

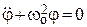. (14)

Решение этого уравнения:

j(t) = A cos( ω_о t + α ) , (15)

где А – амплитуда колебаний, ω_о - циклическая частота колебаний,

α - начальная фаза колебаний.

Период колебаний

(16)

.

В данной работе находится момент инерции. Из формулы (16) следует

. (17)