Введение в обработку результатов измерений

– Мы, кажется, вступили в область догадок, –

заметил доктор Мортимер.

– Скажите лучше – в область, где взвешиваются

все возможности с тем, чтобы выбрать из них наиболее правдоподобную.

А. Конан-Дойль «Собака Баскервилей»

Если подбросить монетку, то она может упасть либо гербом, либо противоположной стороной. Причем выпадение герба или «решки» будет в среднем происходить почти одинаково часто. Говорят, что и то, и другое – события случайные. Такие события принято характеризовать положительным числом – вероятностью события. В приведенном примере события происходят с одинаковой вероятностью, равной 0,5.

Допустим, что кто-то имеет билет лотереи, в которой на каждые 10 билетов приходится один выигрыш. Можно показать, что в этом случае, при достаточно большом числе билетов в лотерее, вероятность выигрыша для каждого билета составляет 0,1, а вероятность того, что он не выиграет – 0,9.

Теория вероятностей дает возможность подсчитать вероятность различных событий. Возникает вопрос, какой должна быть вероятность события, чтобы его наступление можно было считать возможным в реальных условиях? Ответ на этот вопрос носит в значительной мере субъективный характер и зависит от степени важности ожидаемого события.

Известно, что около 5% назначенных концертов отменяется; несмотря на это, мы все же, взяв билет, обычно идем на концерт, будучи, в общем, уверены, что он состоится, хотя вероятность этого всего 0,95. Однако, если бы в 5% полетов терпели аварию пассажирские самолеты, вряд ли мы стали бы пользоваться воздушным транспортом.

Можно указать события, вероятность которых столь мала, что они вообще в мире не происходят и, видимо, не произойдут. Так, вероятность того, что обезьяна, ударяя пальцами по клавишам пишущей машинки, напечатает осмысленное литературное произведение, как показали расчеты, составляет примерно 10^-2600 . Таким же маловероятным (практически невозможным) является так называемое «чудо Джинса» – замерзание воды в чайнике на горячей плите, которое вовсе не противоречит кинетической теории.

Английский математик У. Скарборо предложил модель «случайностей» для экспериментального исследования случайных событий. Лист бумаги нужно разграфить на полосы шириной 1 см, среднюю линию считать «прицельной». Затем взять карандаш двумя пальцами за неотточенный конец и, прицеливаясь в среднюю линию, отпустить (уронить) карандаш с высоты 1м. Карандаш, ударившись о бумагу, оставит след – точку.

Повторяя падение карандаша 25 – 50 раз, получим множество точек, попавших на различные полосы. Построим график разброса точек относительно прицельной линии. Для этого на вертикальной оси отложим число точек, приходящихся на каждую полоску, а по горизонтальной оси – номера полосок (рис.2, а)

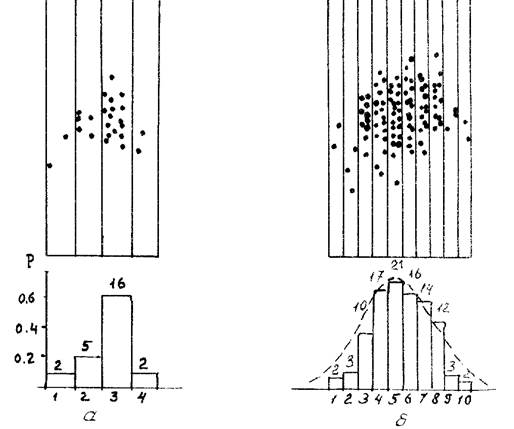
Рис.2. Модель «случайностей». Гистограммы распределения точек по

полосам: а – количество падений n = 25 раз,

б – количество падений n = 100 раз

Получившаяся столбчатая диаграмма носит название гистограммы (histos – столб) распределения (в нашем случае – распределения точек между полосами). На вертикальной оси можно также отложить значения частоты ( 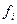) попадания точек на ту или иную полосу.

,

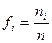где – число точек, попавших на i-ю полосу;

n – общее число падений карандаша на лист бумаги.

Считается, что при достаточном увеличении числа испытаний (бросаний) величины частот 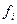становятся устойчивыми и перестают зависеть от общего числа испытаний. Предельные значения этих частот при увеличении числа испытаний до бесконечности называются вероятностями – 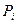. Обратите внимание на то, что сумма вероятностей по всем полоскам .

Если ширину полоски уменьшить, а число падений увеличить, то гистограмма будет несколько иной (рис.2,б). Если продолжить увеличивать число бросков 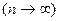, а ширину полоски уменьшать, то гистограмма перейдет в пределе в непрерывную плавную кривую, изображенную на рис.2,б пунктиром. Эта кривая нормального распределения значений случайной величины. – кривая Гаусса. Функция, графически представленная этой кривой, определяет закон распределения значений случайной величины и называется плотностью вероятности.

На практике часто принимают, что случайные погрешности измерения физических величин подчиняются нормальному закону распределения.