Предположим, что существует треугольник АВС, такой, что

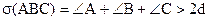. (3)

Используя предыдущие рассуждения, построим треугольник 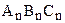, для которого сумма углов равна сумме углов треугольника АВС:

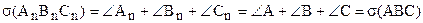, (4)

Угол которого удовлетворяет неравенству (2). При этом выберем число n так, чтобы

.

Тогда из соотношений (2) – (4) следует,

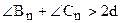. (5)

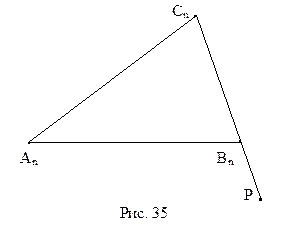Используя теорему 4.1 о внешнем угле треугольника, нетрудно, доказать, что не существует треугольника, сумма двух углов которого больше двух прямых углов. Действительно, пусть 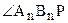- внешний угол при вершине B_n треугольника 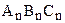(рис. 35). Тогда их теоремы о внешнем угле треугольника следует:

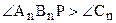. (6)