Рассмотрев свойства дефекта треугольника, мы можем приступить к доказательству второй теоремы Лежандра. Напомним, что доказательство проводится в условиях абсолютной геометрии.
Теорема 10.7. (Вторая теорема Лежандра). Если на плоскости существует хотя бы один треугольник, сумма углов которого равна двум прямым углам, то сумма углов любого другого треугольника также равна развернутому углу.
Доказательство. Нам достаточно доказать, что из равенства нулю дефекта какого либо треугольника на плоскости следует равенство нулю дефекта любого другого треугольника. Прежде всего, докажем это утверждение для прямоугольных треугольников.
Лемма 10.8.Если дефект какого либо прямоугольного треугольника на плоскости равен нулю, то дефект любого другого прямоугольного треугольника также равен нулю.
Доказательство. Пусть АВС – прямоугольный треугольник с прямым углом А, дефект которого равен нулю, М – середина гипотенузы СВ. Построим точки В1, С1 и Р, симметричные точке А относительно точек В, С и М (рис.38).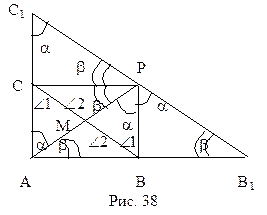 
Обозначим угол САМ через 
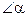, а угол ВАМ – через 
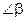. По условию треугольник АВС – прямоугольный, следовательно
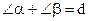. (11)
Ведем также обозначения:
.
Дата добавления: 2015-09-07; просмотров: 814;