Дуговой разряд. 5 страница
Попав в вещество, электроны испытывают сильное торможение и испускают электромагнитные волны (тормозное излучение). Максимальная энергия рентгеновских фотонов соответствует максимальной кинетической энергии электронов Екин = qeU, поэтому по мере увеличения напряжения длина волны, на которую приходится максимум мощности излучения (интенсивности), уменьшается (рис. 14.5).
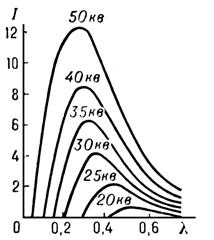
Ритс.14.5.
Спектр тормозного рентгеновского излучения не зависит от природы вещества анода. Согласно классической электродинамике при торможении должны возникать волны всех длин, однако, на опыте установлено, что имеется коротковолновая граница излучения. Объясняет этот факт квантовая теория: величина излучаемого рентгеновского кванта не может превысить энергию, теряемую электроном при торможении hν≤ qeU. Значит, минимальная длина излучаемой волны 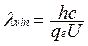 , что соответствует результатам опыта.
, что соответствует результатам опыта.
Когда энергия бомбардирующих электронов становится достаточной для вырывания электронов из внутренних оболочек атома, на фоне тормозного излучения появляются резкие линии характеристического излучения (рис.14.6).
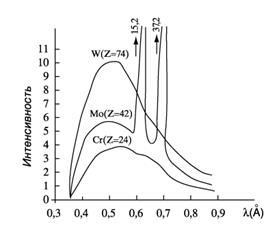
Рис.14.6
Этот тип излучения возникает, когда быстрый электрон, достигая анода, проникает во внутренние орбитали атомов и выбивает один из их электронов. В результате появляется свободное место, которое может быть заполнено другим электроном, спускающимся с одной из верхних атомных орбиталей. Такой переход электрона с более высокого на более низкий энергетический уровень вызывает рентгеновское излучение определенной длины волны. Поэтому характеристическое рентгеновское излучение имеет линейчатый спектр.
Частота линий характеристического излучения зависит от структуры электронных орбиталей атомов анода. Линии спектра характеристического излучения разных химических элементов имеют одинаковый вид, поскольку структура их внутренних электронных орбитальных идентична (рис.14.7).
Рентгеновские спектры состоят из нескольких серий, обозначаемых буквами К, L, M, N, O по наименованию электронной оболочки, на которую совершаются переходы электронов (К – уровень первая ближайшая к ядру оболочка, L – вторая и т.д.). Каждая серия включает небольшое число спектральных линий, обозначаемых в порядке возрастания частоты α, β, γ…. При увеличении атомного номера Z весь рентгеновский спектр смещается в сторону коротких длин волн, не меняя своей структуры, которая одинакова у разных атомов. Разница в частоте объясняется энергетическим различием между внутренними орбиталями легких и тяжелых атомов.
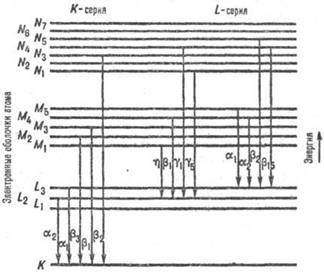
Рис.14.7
Частота линий спектра характеристического рентгеновского излучения определяется законом Мозли: корень квадратный из частоты является линейной функцией атомного номера
ν1/2=A(Z-σ), где Z - атомный номер химического элемента, A и - σ константы.
Закон Мозли позволяет по длине излучаемой рентгеновской волны определять атомный номер элемента, на этом основан рентгеноспектральный анализ веществ.
5. Люминесценция — нетепловое свечение вещества, происходящее после поглощения им энергии возбуждения. В зависимости от вида поглощаемой энергии люминесценция делится на виды:
· фотолюминесценция — свечение вещества под действием света; хемилюминесценция — свечение, использующее энергию химических реакций (окисление фосфора на солнце, гниющее дерево, светлячки и т.п.);
· катодолюминесценция — вызвана облучением быстрыми электронами (катодными лучами) твердых тел (свечение экрана электронно-лучевого телевизора);
· электролюминесценция- возникает под действием электрического поля – при прохождении тока, под действием разряда и т. п.
Фотолюминесценция делится на флуоресценцию и фосфоресценцию. Флуоресценция – это свечение вещества практически в момент его возбуждения светом, оно прекращается при выключении света. Фосфоресценция - это послесвечение, продолжается после выключения света.
Цвет возникающего свечения является характерным признаком люминесценции, он отличается от цвета возбуждающего света. В 1852 году Стоксом установлено правило: свет люминесценции характеризуется большей длиной волны, чем поглощаемый телом свет (рис.14.8). Обычно спектральная полоса поглощения и полоса люминесценции частично перекрываются.
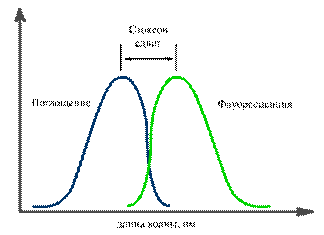
Рис.14.8
Правило Стокса находит объяснение с позиции квантовой теории. Энергия поглощенного фотона большей частью преобразуется в энергию фотона люминесценции, но часть энергии А тратится на внутримолекулярные процессы. По закону сохранения энергии hνлюм = hνпогл – А.
Независимо от способа возбуждения и длины волны возбуждающего света спектр люминесценции остается неизменным при данной температуре. Объясняется это стабильностью разрешенных энергетических уровней в атоме/молекуле и позволяет проводить люминесцентный анализ состава веществ. Люминесцентный метод весьма чувствительный, сего помощью можно обнаружить 10 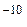 г вещества.
г вещества.
6. Лазерное излучение – это вынужденное монохроматическое излучение оптических квантовых генераторов (ОКГ). Квантовые генераторы электромагнитного излучения принято называть лазерами (Light Amplification by Stimulated Emission of Radiation – усиление света с помощью вынужденного излучения). Идея лазера предложена в 1951 году Н.Г.Басовым и А.М.Прохоровым, первый твердотельный лазер на рубине создан Мейманом в 1960 году и газовый лазер создан на смеси неона и гелия в 1961 году в США.
Эйнштейн показал, что под действием внешнего электромагнитного поля может происходить переход электрона из возбужденного состояния Евозб в основное Еосн. Происходящее при этом излучение называется вынужденным или индуцированным, причем такое излучение возникает, если частота поля
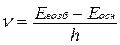
В квантовых генераторах используется вещество, имеющее, помимо основного уровня энергии и уровня возбуждения, третий уровень – уровень задержки, расположенный между ними. Исторически первым таким веществом стал кристалл рубина (рис.14.9).

Рис.14.9
Схема устройства рубинового лазера приведена на рис. 14.10. Рабочее тело (активную среду) лазера представляет собой рубиновый цилиндр, на торцах которого имеются зеркала, установленные строго параллельно друг другу.
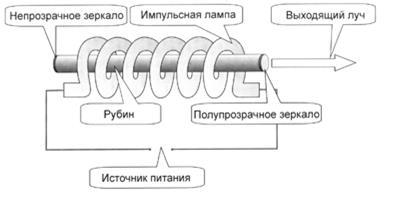
Рис.14.10
Под действием энергии излучения импульсной лампы накачки электроны в рубине переходят с основного уровня Е0 на уровень возбуждения Е2
(рис.14.11 а)
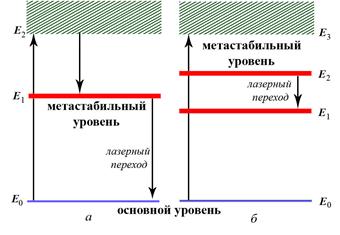
Рис.14.11
В твердом теле отдельные разрешенные уровни атомов объединяются в зону в результате взаимодействия атомов кристаллической решетки.
Через 10 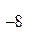 с электроны отдают часть энергии кристаллической решетке и опускаются на уровень с меньшей энергией Е1, задерживаясь на нем на время 3·10
с электроны отдают часть энергии кристаллической решетке и опускаются на уровень с меньшей энергией Е1, задерживаясь на нем на время 3·10 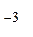 с. Такой метастабильный уровень создается путем введения в кристалл рубина примеси – небольшого количества ионов хрома. В результате происходит насыщение примесного уровня Е1 электронами.
с. Такой метастабильный уровень создается путем введения в кристалл рубина примеси – небольшого количества ионов хрома. В результате происходит насыщение примесного уровня Е1 электронами.
При любом переходе электрона с метастабильного уровня на основной уровень испускается квант света с частотой
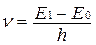 ;
;
этот квант вызывает вынужденный переход другого электрона с метастабильного уровня на основной уровень также с излучением кванта света с той же частотой. Процесс формирования лазерного луча условно показан на рис.14.12.
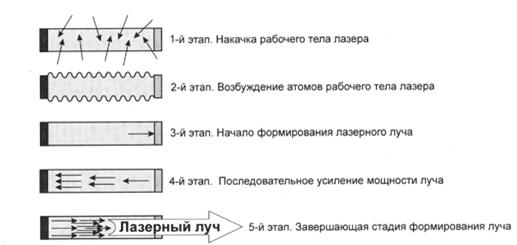
Рис.14.12
Интенсивность лазерного луча постепенно нарастает, отражаясь от зеркал на торцах, луч многократно усиливается и, достигнув определенной мощности, выходит из полупрозрачного зеркала. Кванты света, направленные под углом к оси рабочего тела – резонатора не усиливаются, они поглощаются боковой поверхностью.
Все лучи, выходящие из лазера, практически параллельны, имеют очень малый угол расхождения. Мощность излучения в импульсном режиме может достигать 10 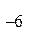 Вт/см².
Вт/см².
Теоретически излучение лазера должно быть строго монохроматичным, определенной частоты. Однако, спектр излучения лазера имеет малую, но конечную ширину δν . Небольшой набор частот зависит от длительности импульса, длины резонатора, показателя преломления среды.
В газовых, полупроводниковых, жидкостных лазерах возбуждение излучения осуществляется с помощью электрического разряда.
 |  |
В 1963 г. Ж. Алфёров и Г. Кремер (Нобелевская премия по физике 2000 г.) разработали теорию полупроводниковых гетероструктур, на основе которых были созданы многие полупроводниковые лазеры (рис.14.13).
Рис.14.13
Полупроводниковые лазеры могут иметь очень малые размеры (~ 0,1 мм в длину), однако, расхождение луча у них больше. Спектральные характеристики полупроводникового лазера зависят от свойств применяемых материалов.
Свойства лазерного излучения:
- излучение когерентно и практически монохроматично; это дало возможность освоить диапазон видимого света для осуществления передачи информации и связи, тем самым существенно увеличив количество передаваемой информации в единицу времени.
- малая расходимость луча; из-за того, что вынужденное излучение распространяется строго вдоль оси резонатора, лазерный луч расширяется слабо: его расходимость составляет несколько угловых секунд, это позволяют фокусировать лазерный луч в пятно очень малого размера, с огромную плотностью энергии.
- в импульсе лазерное излучение может иметь большую мощность и огромную температуру;
например, импульсный лазер мощностью порядка петаватта (1015 Вт) имеет температуру излучения около 100 миллионов градусов.
Применение лазеров.
Технологические лазеры. Мощные лазеры непрерывного действия применяются для резки, сварки и пайки деталей из различных материалов. Высокая температура излучения позволяет сваривать материалы, которые иными методами соединить нельзя (например, металл с керамикой). Высокая монохроматичность излучения позволяет сфокусировать луч в точку диаметром порядка микрона и применять его для изготовления микросхем (так называемый метод лазерного скрайбирования – снятия тонкого слоя).
В геодезии и строительстве импульсные лазеры применяют для измерения расстояний на местности, рассчитывая их по времени движения светового импульса между двумя точками. Точные измерения в промышленности производят при помощи интерференции лазерных лучей, отраженных от концевых поверхностей изделия.
Лазерная связь.Существует простая закономерность: чем выше несущая частота (меньше длина волны) канала связи, тем больше информации за единицу времени можно через него передать. Свет – такая же электромагнитная волна, как и радиоволны, только в десятки тысяч раз короче, поэтому по лазерному лучу можно передать в десятки тысяч раз больше информации, чем по высокочастотному радиоканалу. Лазерная связь осуществляется по оптическому волокну практически без потерь на многие сотни километров. Лазерным лучом записывают и воспроизводят изображение (в том числе движущееся) и звук на компакт-дисках.
Лазеры в медицине.Хирургические операции, производимые «лазерным скальпелем» меньше травмируют живые ткани. А лазерное излучение малой мощности ускоряет заживление ран и оказывает воздействие, аналогичное иглоукалыванию, практикуемому восточной медициной (лазерная акупунктура).
Лазеры в научных исследованиях.Чрезвычайно высокая температура излучения и высокая плотность его энергии дает возможность исследовать вещество в экстремальном состоянии, существующем только в недрах горячих звезд. Делаются попытки осуществить термоядерную реакцию, сжимая ампулу со смесью дейтерия с тритием системой лазерных лучей (т.н. инерционный термоядерный синтез). В генной инженерии и нанотехнологии (технологии, имеющей дело с объектами с характерными размерами 10–9 м) лазерными лучами разрезают, передвигают и соединяют фрагменты генов, биологических молекул и детали размером порядка миллионной доли миллиметра (10–9 м). Лазерные локаторы (лидары) применяются для исследования атмосферы.
Военные лазеры. Военное применение лазеров включает как их использование для обнаружения целей и связи, так и применение в качестве оружия. Лучами мощных химических и эксимерных лазеров наземного или орбитального базирования планируется разрушать или выводить из строя боевые спутники и самолеты противника. Созданы образцы лазерных пистолетов для вооружения экипажей орбитальных станций военного назначения.
ЛЕКЦИЯ 15
Тема:Элементы квантовой механики
Вопросы:1) Волновые свойства вещества. Гипотеза де Бройля
2) Принцип неопределенности
3) Уравнение Шредингера. Частица в одномерной потенциальной яме
4) Атом водорода по квантово-механической теории
5) Квантовая статистика электронов в металлах и полупроводниках
1. В начале 20-го века стало уже ясно, что свет проявляет двойственные свойства, т.е. дуализм. Волновая природа его проявляется в интерференции и дифракции, а корпускулярная – в фотоэффекте, эффекте Комптона.
В 1924 году Луи де Бройль выдвинул гипотезу, что дуализм имеет универсальное значение и присущ также и частицам. Так, фотон обладает энергией Е = hν и импульсом 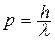 . По идее де Бройля движение электрона или любой другой частицы связано с волновым процессом, т.е. частицам присуща волна с длиной
. По идее де Бройля движение электрона или любой другой частицы связано с волновым процессом, т.е. частицам присуща волна с длиной 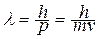 .
.
 |  |
В 1927 году гипотеза де Бройля подтвердилась рядом экспериментов. Так, в 1927 году Томсон направлял пучок электронов, ускоренных разностью потенциалов порядка десятков киловольт, на тонкую металлическую фольгу рис.15.1). Пройдя через фольгу, электроны давали на фотопластинке такую же дифракционную картину, как и рентгеновские фотоны.
Рис.15.1
Полученные в опытах длины волн соответствуют длине волны де Бройля. Опыты показали, что дифракционная картина наблюдается даже при небольшом числе электронов в пучке и волновые свойства присущи отдельному электрону.
Дифракционные явления наблюдались также у пучков атомов и молекул, т.е. волновые свойства присущи всем микрочастицам – молекулам, атомам, нейтронам, протонам и другим элементарным частицам. Однако, эти волны отличаются от обычных волн – их нельзя разделить на части, например, отражением и преломлением. Частица ведет себя как неделимое целое.
2. В классической механике состояние частицы определяется значением координат, импульса, энергии. Применяя законы динамики можно рассчитать траекторию движения частицы и ее местонахождение в любой момент времени.
Наличие волновых свойств, необычное поведение микрочастиц не позволяют определять их состояние методами классической механики. Нельзя говорить об определенной траектории микрочастицы и нельзя одновременно точно определить значение координаты и импульса частицы в любой момент времени. Это обстоятельство отражает одно из основных положений квантовой механики – соотношение неопределенностей Гейзенберга: произведение неопределенностей двух сопряженных переменных величин не может быть меньше постоянной Планка
ΔxΔpx ≥ h;
ΔyΔpy ≥ h;
ΔzΔpz ≥ h.
Соотношение неопределенностей означает, что, если попытаться точно определить координату микрочастицы в какой-то момент времени (Δx = 0), то погрешность (неопределенность) определения импульса частицы становится бесконечно большой. Так как импульс частицы p = mv, то соотношение неопределенностей можно записать в виде ΔxΔvx ≥ h/m. Значит, чем больше масса частицы, тем меньше неопределенность ее координаты и импульса. Поэтому принцип Гейзенберга, как и гипотеза де Бройля, применимы к микрочастицам и не проявляются в макромире.
Соотношение неопределенностей для энергии микрочастицы и времени имеет такой же вид:
ΔEΔt ≥ h.
Соотношение показывает, что для определения энергии частицы с точностью ΔE потребуется интервал времени не меньше Δt.
Соотношение неопределенностей допускает существование виртуальных частиц, которые имеют очень короткое время жизни, но не могут быть зафиксированы никакими приборами. Их параметры можно оценить с помощью законов сохранения в различных процессах взаимодействия микрочастиц. Соотношение неопределенностей объясняет, почему электрон не падает на ядро – в этом случае его координаты и импульс приобрели бы определенные значения, что не может осуществиться в микромире.
3. Дифракционная картина для электронов, прошедших через фольгу (рис.15.1) показывает, что электроны попадают на фотопластинку в местах максимума интенсивности волн де Бройля неравномерно. Наблюдается статистическое распределение частиц, которое необходимо описывать понятиями теории вероятности. Вероятностный подход положен в основу квантовой механики, он наиболее точно отражает процессы в микромире.
В 1926 году Шредингер вывел основное уравнение квантовой механики, в котором сопоставил движению микрочастицы комплексную функцию координат и времени ψ (пси-функция). Пси – функцию он назвал волновой функцией.
Для стационарных состояний частицы уравнение Шредингера имеет вид
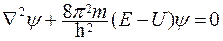 ,
,
где Е – полная энергия электрона, U - потенциальная энергия; 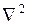 - оператор
- оператор
Лапласа
 |  |
Смысл пси-функции состоит в том, что квадрат ее модуля определяет вероятность того, что частица будет обнаружена в данной точке пространства. Квантовая механика не позволяет определить местонахождение частицы в пространстве и ее траекторию. С помощью пси-функции можно только предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. Уравнение Шредингера позволяет найти пси функцию для заданных условий и определить вероятность нахождения частицы в различных точках пространства.
Пусть частица находится в бесконечно глубокой одномерной потенциальной яме. Понятие потенциальной ямы означает, что на частицу действует сила, не позволяющая ей оторваться от источника силы и стать свободной. Например, электрон в атоме движется в поле притяжения ядра в ограниченном пространстве, т.е. находится в потенциальной яме.
 |
Чтобы упростить рассуждения, будем считать, что частица движется вдоль оси Х между бесконечно высокими энергетическими стенками (рис.15.2).
Рис.15.2
Расстояние между стенками l, между стенками U = 0 при 0 ≥ х ≤ l.
За стенками U = ∞ при х <0 и х > l .
Для рассматриваемого случая уравнение Шредингера имеет вид
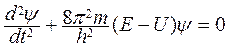
Так как за пределы ямы частица не может попасть, то ψ(0) = ψ(l) = 0 – граничные условия. Внутри ямы U = 0, поэтому уравнение Шредингера можно записать в виде
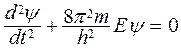 .
.
Обозначим 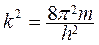 , тогда уравнение примет вид
, тогда уравнение примет вид 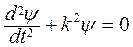 . Решение дифференциального уравнения получаем в виде ψ(х) = Аsin(kx +α).
. Решение дифференциального уравнения получаем в виде ψ(х) = Аsin(kx +α).
Из условия, что ψ(0) = 0, получим Аsinα = 0. Отсюда α = 0. Из условия, что ψ(l) = 0, получим Аsinkl = 0. Это возможно при kl = ±nπ, где n = 1,2,3…
Так как 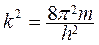 , то
, то 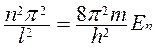 . Отсюда получаем ряд значений энергии, которую может иметь частица в потенциальной яме
. Отсюда получаем ряд значений энергии, которую может иметь частица в потенциальной яме
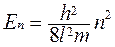 , где n = 1,2,3…
, где n = 1,2,3…
Таким образом, частица в силовом поле имеет дискретный ряд определенных значений энергии, а волновая функция также принимает ряд значений
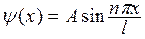
Вид волновой функции для трех значений числа n показан на рис.15.3.
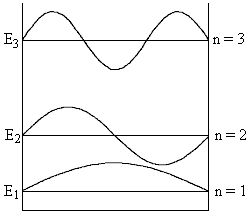
Рис.15.3
4. Рассмотрим атом, в котором электрон движется вокруг ядра (атом водорода или ион гелия). Потенциальная энергия электрона в поле ядра
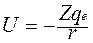 ,
,
здесь Z – порядковый номер атома, r - расстояние электрона от ядра.
Уравнение Шредингера имеет вид
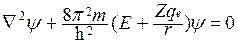 .
.
Из решения этого уравнения вытекает, что энергия электрона принимает дискретные значения 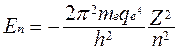 , где n = 1,2,3…Число n называется главным квантовым числом. Оно совпадает с номером уровня энергии, характеризует величину энергии электрона в атоме.
, где n = 1,2,3…Число n называется главным квантовым числом. Оно совпадает с номером уровня энергии, характеризует величину энергии электрона в атоме.
Поскольку понятие траектории электрона в атоме в представлениях квантовой механики теряет смысл, то говорят об области пространства вблизи ядра, где электрон появляется с наибольшей вероятностью. Это облако вероятности или, как его обычно называют, электронное облако.
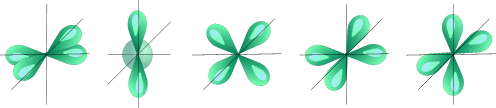
Рассматривая момент импульса электрона в атоме, квантовая механика показывает, что он также принимает дискретный ряд значений, который определяется азимутальным квантовым числом l = 0, 1, 2, 3,…n – 1. Состояния с различными значениями азимутального квантового числа отличаются величиной момента импульса, т.е. формой электронного облака. Электрон в состоянии с l = 0 условно обозначают s- электроном (форма электронного облака сферическая на рис.15.4а), в состоянии с l = 1 обозначают p – электроном (форма облака гантелеобразная на рис.15.4б), в состоянии с l = 2 обозначают d – электроном (рис.15.4в), в состоянии l = 3 обозначают f – электроном.
 |

а б
в
Рис. 15.4
При определенном значении азимутального квантового числа вытянутые p-, d-, f- электронные облака могут принимать только определенные положения в пространстве, которые задаются магнитным квантовым числом m = -l, -l +1, …-2, -1, 0, 1, 2, …l -1, l. Так, для l = 1 магнитное квантовое число принимает значения m = -1, 0, 1, т.е. р – облако может иметь три ориентации в пространстве (рис.15.4 б). Для l = 2 магнитное квантовое число принимает значения m = -2, -1, 0, 1, 2 т.е. d – облако имеет пять ориентаций в пространстве (рис.15.4 в).
Схема энергетических уровней электрона в атоме водорода изображена на рис.15.5.
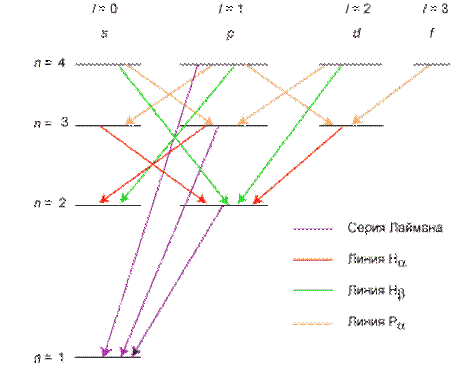
Рис.15.5
Испускание и поглощение света происходит при переходах электрона с одного энергетического уровня на другой. Квантовая механика показывает, что такие переходы возможны только, если выполняется правило отбора для азимутального квантового числа Δl = ± 1. Значит возможны только такие переходы, при которых l изменяется на единицу (рис.15.5).
В электронных формулах, обозначающих состояния электрона, на первом месте ставится главное квантовое число, затем обозначение азимутального квантового числа. В атоме водорода возможны состояния электрона (рис.15.6):

1s
2s, 2p
3s, 3p, 3d
4s, 4p, 4d, 4f
……………
Рис.15.6
В многоэлектронных атомах главное квантовое число обозначает также номер электронной оболочки, в которую входят электроны с различными азимутальными и магнитными квантовыми числами. Для объяснения их спектров пришлось ввести еще спиновое квантовое число ms = ± ½.
5. В настоящее время отсутствуют методы точного решения динамической задачи для системы многих частиц. Поэтому использование уравнения Шредингера для задачи о взаимодействии множества электронов и ядер в твердом теле не позволяет найти точных решений. Эта задача решается приближенно, путем сведения задачи многих частиц к одноэлектронной задаче об одном электроне, движущемся в заданном внешнем поле. Подобный путь приводит к зонной теории твердого тела.
Рассмотрим мысленно «процесс образования» твердого тела из изолированных атомов одного типа. Энергетические уровни какого-либо валентного электрона в одном изолированном атоме представлены на схематическом рис.15.7 (а). Для простоты будем считать их простыми, т. е. невырожденными.

Рис.15.7
Рассмотрим теперь N тождественных атомов, удаленных друг от друга настолько далеко, что их взаимодействием можно полностью пренебречь. Энергетические уровни того же валентного электрона системы N невзаимодействующих атомов получатся, если рисунок (а) повторить N раз — столько, сколько содержится атомов в системе (рис.15.7, б). Теперь каждый простой уровень превращается в уровень кратности N.
Будем сближать атомы друг с другом, чтобы они образовали кристаллическую решетку. из-за взаимодействия между атомами каждый кратный энергетический уровень расщепится на N простых уровней (рис.15.8).

Рис.15.8
Совокупность энергетических уровней, на которые расщепляется кратный уровень, называется энергетической зоной или просто зоной кристалла (см. рис.15.9). Ввиду того, что N очень велико, расстояния между уровнями одной и той же зоны крайне малы, так что требуется ничтожная энергия, чтобы перевести электрон в пределах зоны с одного энергетического уровня на соседний. В этом смысле энергетические уровни каждой зоны ведут себя практически так, как если бы они были непрерывны. Однако соседние энергетические зоны, вообще говоря, разделены конечными интервалами энергии. Эти интервалы называются запрещенными зонами, так как энергия электрона не может принимать значения, лежащие в пределах таких интервалов. Зоны с дозволенными значениями энергии называются разрешенными. Величина расщепления для разных уровней не одинакова. Сильнее возмущаются уровни, заполненные в атоме внешними электронами.
Дата добавления: 2015-09-18; просмотров: 703;
