Дуговой разряд. 2 страница
Основной закон электромагнитной индукции: эдс электромагнитной индукции пропорциональна быстроте изменения магнитного потока через площадь, ограниченную контуром
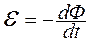 .
.
Знак минус соответствует закону Ленца. Как видно из рис.7.3, направление нормали n и выбранное положительное направление обхода контура l связаны правилом правого буравчика.
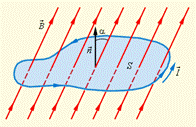
Рис.7.3 Магнитный поток через замкнутый контур.
Если магнитное поле увеличивается, т.е. 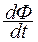 >0, то
>0, то 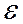 < 0, а значит и индукционный ток I< 0. Это означает, что направление индукционного тока противоположно выбранному положительному направлению.
< 0, а значит и индукционный ток I< 0. Это означает, что направление индукционного тока противоположно выбранному положительному направлению.
Явление электромагнитной индукции положено в основу работы генераторов электрического тока, электрических двигателей, трансформаторов и других электротехнических устройств.
Пример.Пусть в однородном магнитном поле находится проводник в виде замкнутого контура. Магнитный поток через контур Ф =В Scosα. Если контур вращается с постоянной угловой скоростью 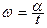 , то Ф =ВScosωt. Значит, при вращении контура магнитный поток через него меняется и в контуре возникает эдс индукции
, то Ф =ВScosωt. Значит, при вращении контура магнитный поток через него меняется и в контуре возникает эдс индукции
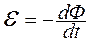 = В Sωsinωt,
= В Sωsinωt,
и течет синусоидальный (переменный) ток 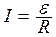 =
= 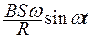 .
.
2. Пусть в проводнике в виде катушки течет ток (рис.7.4).

Рис.7.4
Величина магнитной индукции в любой точке поля пропорциональна величине тока, а значит, и магнитный поток, пронизывающий катушку, пропорционален току
Ф = LI.
Коэффициент пропорциональности L называется индуктивностью контура. Единицей индуктивности служит генри (Гн). 1 Гн = 1 Вб/А.
Индуктивность проводников зависит от их размеров, формы, от магнитной проницаемости среды. Так, индуктивность проводника в виде катушки равна
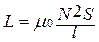 ,
,
где N - число витков катушки, l - длина катушки, S - площадь поперечного сечения катушки.
При изменении тока меняется магнитный поток через витки катушки, поэтому в катушке возникает эдс индукции и индукционный ток. Явление возникновение дополнительного индукционного тока в проводнике при всяком изменении основного тока называется самоиндукцией. Величина эдс самоиндукции
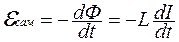
пропорциональна быстроте изменения тока.
Пусть имеется электрическая цепь (рис.7.5) с двумя лампочками Л1 и Л2, подключенными к источнику тока. К лампочке Л1 подключена последовательно катушка индуктивности.
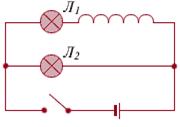
Рис.7.5
При разомкнутом ключе тока нет, и лампочки не светятся. Если ключ замкнуть, то медленнее загорается лампочка Л1., так как при нарастании тока в катушке индуктивности появляется эдс самоиндукции и течет индукционный ток, направленный против основного тока (препятствует нарастанию тока). При установившемся значении основного тока индукционный ток исчезает.
При размыкании ключа ток уменьшается и в катушке возникает индукционный ток такого же направления (препятствует уменьшению тока). Чем быстрее изменяется основной ток, тем больше величина индукционного тока (экстратока). Лампочка Л1 при этом ярко вспыхивает и гаснет позже Л2.
3. Рассмотрим электрическую цепь, изображенную на рис.7.6.
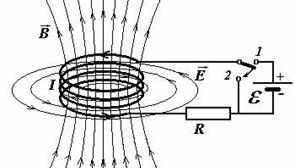
Рис.7.6
В положении 1 ключа через катушку течет постоянный ток и существует магнитное поле В этого тока. Если замкнуть ключ в положение 2, разомкнув 1, то через сопротивление потечет убывающий ток, поддерживаемый эдс самоиндукции. Работа тока за время dt равна dA = 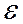 сам q =
сам q = 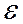 сам Idt. Так как
сам Idt. Так как
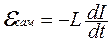 , то dA = -LIdI.
, то dA = -LIdI.
Проинтегрируем от до нуля и получим работу за время исчезновения магнитного поля
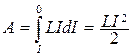
Работа идет на приращение внутренней энергии, то есть на нагревание сопротивления, проводов, катушки. Совершение работы сопровождается уменьшением магнитного поля, больше ничего не меняется, значит, работу совершает магнитное поле за счет своей энергии. Таким образом, энергия магнитного поля
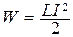
Можно показать, что 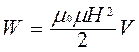 , где V – объем поля. Плотность энергии магнитного поля
, где V – объем поля. Плотность энергии магнитного поля
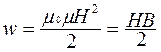
ЛЕКЦИЯ 8
Тема:Электромагнитные колебания
Вопросы:1) Свободные колебания в контуре без активного сопротивления
2) Свободные затухающие электромагнитные колебания
3) Вынужденные электромагнитные колебания.
1. Цепь, содержащая индуктивность и емкость, называется колебательным контуром (рис.8.1). Сопротивление контура считаем пренебрежимо малым.
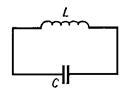
Рис.8.1
Если зарядить конденсатор и отключить источник, то вся энергия контура в начальный момент времени сосредоточена в электрическом поле конденсатора (рис.8.2).
t = 0 t = T/4 t = T/2 t = 3T/4 t = T

Рис.8.2
В первую четверть периода растет ток разрядки конденсатора, этот ток в катушке индуктивности создает возрастающий магнитный поток. Магнитный поток пронизывает витки катушки и порождает в них ток самоиндукции, направленный против основного тока (препятствует его возрастанию). В конце первой четверти периода ток достигает максимума Im и вся энергия теперь сосредоточена в магнитном поле. Заряда в конденсаторе нет, поэтому ток во второй четверти периода уменьшается, и ток самоиндукции меняет направление – теперь он направлен в ту же сторону, что и основной ток (препятствует его уменьшению). Этот ток самоиндукции перезаряжает конденсатор и в конце второй четверти периода энергия снова в электрическом поле, а ток равен нулю. Далее процесс повторяется в обратную сторону и за период заряд на обкладках конденсатора совершит полное колебание, как и ток в катушке индуктивности.
Из закона сохранения энергии следует, что электрическое и магнитное поля совершают одинаковую работу, т.е. U = 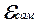 , где напряжение на конденсаторе U = q/C, а
, где напряжение на конденсаторе U = q/C, а 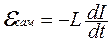 . Значит,
. Значит, 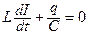 . Подставим
. Подставим 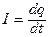 и разделим на L, получим
и разделим на L, получим
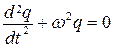 , где обозначили
, где обозначили 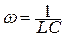 .
.
Это дифференциальное уравнение является уравнением свободных незатухающих электромагнитных колебаний в контуре. Решение этого уравнения q = q0cos(ωt +α 0) описывает гармонические колебания заряда на обкладках конденсатора. Амплитуда заряда q0 , циклическая частота ω = 2πν, частота колебаний 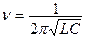 , период колебаний
, период колебаний 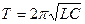 .
.
Напряжение на конденсаторе создается зарядом и изменяется так же:
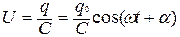 = Umcos(ωt+α ), где Um - амплитуда напряжения.
= Umcos(ωt+α ), где Um - амплитуда напряжения.
Сила тока в контуре
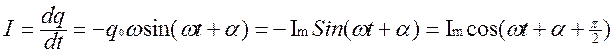
где Im - амплитуда тока, α – начальная фаза. Из соотношения фаз видно, что ток опережает напряжение на конденсаторе на π/2. При нулевом напряжении ток максимальный.
Из сравнения амплитуд тока и напряжения вытекает 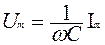 , т.е. амплитуды связаны законом Ома, где
, т.е. амплитуды связаны законом Ома, где 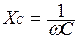 представляет собой емкостное сопротивление цепи.
представляет собой емкостное сопротивление цепи.
Напряжение на катушке индуктивности должно быть равно ЭДС самоиндукции и противоположно к ней направлено:
U = - 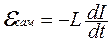 = LωImcos (ωt+α ) = LωImsin (ωt+α +π/2)
= LωImcos (ωt+α ) = LωImsin (ωt+α +π/2)
Из соотношения фаз видно, что ток в катушке индуктивности отстает от напряжения на π/2. Амплитуды тока и напряжения связаны соотношением Um=Im. В этом случае XL = ωL представляет собой индуктивное сопротивление цепи.
2. Всякий реальный колебательный контур обладает сопротивлением R (рис.8.3) и при протекании тока в проводниках выделяется джоулево тепло. Поэтому, если один раз зарядить конденсатор, то запасенная энергия расходуется на тепло и колебания затухают.
3.
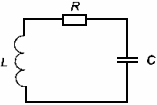
Рис.8.3
Так как источника ЭДС в цепи нет, то применяя второй закон Кирхгофа к цепи, получим UL+UR+UC = 0. После подстановки получаем
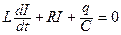
Выразим ток через заряд и разделим уравнение на L. Получим дифференциальное уравнение свободных затухающих колебаний
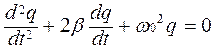
Здесь 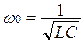 собственная частота колебательного контура,
собственная частота колебательного контура, 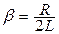 коэффициент затухания. Решение полученного уравнения (рис.8.4)
коэффициент затухания. Решение полученного уравнения (рис.8.4)
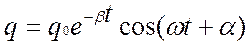 , где q0 – величина заряда в начальный момент времени, частота затухающих колебаний
, где q0 – величина заряда в начальный момент времени, частота затухающих колебаний 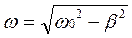 , т.е.
, т.е. 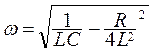 .
.
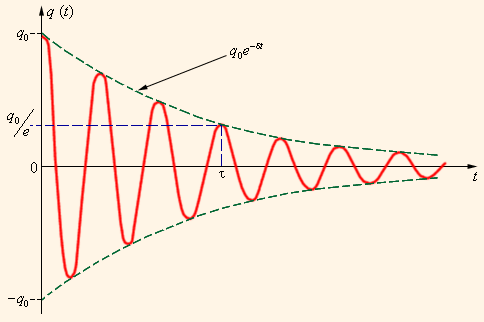
Рис.8.4
Время затухания τ – это время, за которое заряд на обкладках конденсатора уменьшается в е = 2,7 раз. τ = 1/β, т.е. τ = 2L/R.
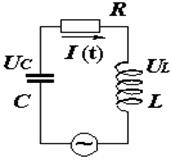
3. Колебания, происходящие в электрической цепи под действием внешней периодической эдс, называются вынужденными. Это действие может быть оказано через индуктивную связь двух катушек индуктивности (взаимная индукция) или непосредственным включением переменного напряжения
U = Umcosωt в колебательный контур (рис.8.5).
U
Рис.8.5
Применяя второй закон Кирхгофа к цепи, получим UL+UR+UC = Umcosωt, или 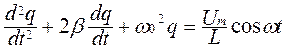 . Здесь ω – частота переменного напряжения,
. Здесь ω – частота переменного напряжения, 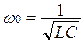 - собственная частота колебательного контура,
- собственная частота колебательного контура, 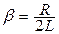 - коэффициент затухания.
- коэффициент затухания.
Решение уравнения дает q = q mcos (ωt – φ), где амплитуда заряда
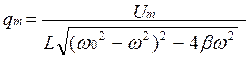 ;
; 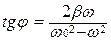 .
.
При некоторой частоте внешнего напряжения амплитуда колебаний резко возрастает, т.е. возникает резонанс. Чтобы определить резонансную частоту, нужно найти максимум функции q(ω), т.е. минимум выражения под корнем в знаменателе. Для этого продифференцируем выражение и получим
-4(ω0² – ω²) ω + 8β²ω = 0. Уравнение имеет три решения для ω: ω = 0 и 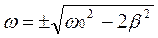 . ω = 0 соответствует максимуму знаменателя, а отрицательная частота не имеет смысла, поэтому
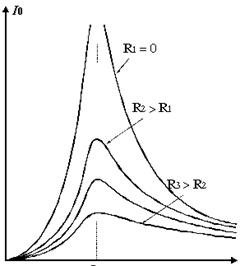
. ω = 0 соответствует максимуму знаменателя, а отрицательная частота не имеет смысла, поэтому 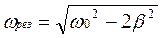 . Чем меньше β, т.е. меньше сопротивление контура, тем выше и острее максимум резонансной кривой для тока (рис.8.6).
. Чем меньше β, т.е. меньше сопротивление контура, тем выше и острее максимум резонансной кривой для тока (рис.8.6).
Уравнение для тока получим, продифференцировав выражение для заряда: I = - ω q msin (ωt – φ) или I = Imcos (ωt – φ +π/2). Ток и заряд изменяются в противофазе, когда заряд на конденсаторе достигает максимума, ток в цепи равен нулю и наоборот.
 ω
ω
ωрез
Рис.8.6
Для напряжений в каждый момент времени выполняется соотношение
UL+UR+UC = Umcosωt.
Напряжение на резисторе UR = IR, UR = RImsin (ωt – φ). Ток в резисторе изменяется в одной фазе (синфазно) с напряжением.
Напряжение на конденсаторе
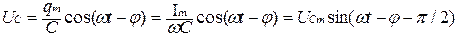 .
.
Напряжение на конденсаторе и ток также изменяются в противофазе, причем ток опережает напряжение на π/2.
Напряжение на индуктивности
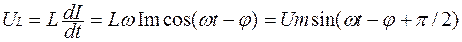
В этом случае ток отстает от напряжения на π/2.
Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм. На векторной диаграмме колебания определенной заданной частотыω изображаются с помощью векторов. Длины векторов на диаграмме равны амплитудам колебаний, а наклон к горизонтальной оси определяется фазами колебаний φ1 и φ2. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ1 – φ2. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов.
Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи. На рис.8.7 показана векторная диаграмма для напряжений на участках рассмотренного колебательного контура (амплитуда тока обозначена I0).
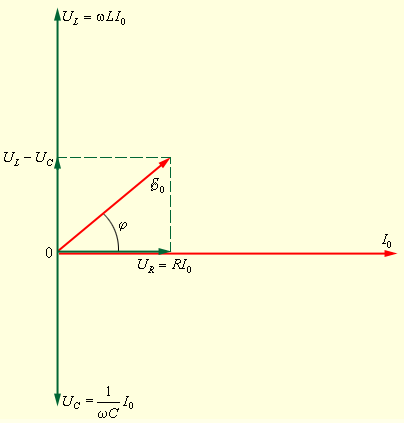
Рис. 8.7 Векторная диаграмма для последовательной RLC-цепи
Амплитуды токов и напряжений связаны законом Ома, поэтому XL = ωL называют индуктивным сопротивлением, а 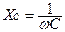 - емкостным сопротивлением. Полное электрическое сопротивление последовательной RLC- цепи синусоидального тока
- емкостным сопротивлением. Полное электрическое сопротивление последовательной RLC- цепи синусоидального тока 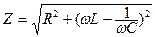 .
.
ЛЕКЦИЯ 9
Тема:Теория Максвелла. Электромагнитные волны.
Вопросы:1) Теория Максвелла
2) Электромагнитные волны, получение и свойства
3) Шкала электромагнитных волн
1. В шестидесятых годах девятнадцатого века профессор кембриджского университета Джеймс Максвелл опубликовал «Динамическую теорию поля», созданную на основе анализа всех открытых к тому времени явлений электричества и магнетизма. Максвелл пришел к выводу, что в явлении электромагнитной индукции наличие проводника не имеет существенного значения (ЭДС индукции не зависит от природы проводника), и сформулировал первое основное положение своей теории: всякое изменение магнитного поля вызывает появление вихревого электрического поля (рис.9.1).
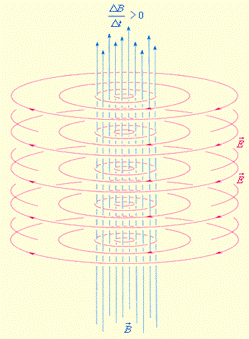
Рис. 9.1
Электрическое поле динамическое и вызывает в любом проводнике движение электронов по замкнутым траекториям. Значит, вихревое электрическое поле выполняет роль сторонней силы в выражении электродвижущей силы для вихревых токов в проводниках
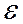 =
= 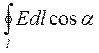
Эта ЭДС вызвана изменением магнитного поля 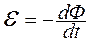 , поэтому математическое выражение первого основного положения теории Максвелла имеет вид
, поэтому математическое выражение первого основного положения теории Максвелла имеет вид
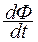 =
= 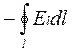
Вихревые токи в массивных проводниках сопровождаются выделением большого количества джоулева тепла, поэтому нашли полезное применение в индукционных печах. В электротехнических устройствах (трансформаторах, двигателях, генераторах) на вихревые токи бесполезно тратится электрическая энергия, поэтому токи называют паразитными и подавляют их, набирая магнитопроводы (сердечники, корпуса) из тонких пластин, изолированных лаком.
Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями
в диэлектриках или вакууме. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
Рассмотрим цепь переменного тока, содержащую конденсатор (рис.9.2).
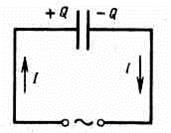
Рис.9.2
Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, замыкающее электрическую цепь. Если включить в цепь лампочку, то она будет гореть. Через конденсатор «протекает» ток смещения. Током смещения была названа Максвеллом величина, пропорциональная скорости изменения электрического поля во времени. Ток смещения возбуждает такое же магнитное поле, что и ток проводимости в проводах (позднее это было подтверждено экспериментально) (рис.9.3).
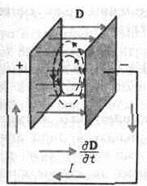
Рис.9.3
Полный ток в цепи переменного тока, равный сумме тока проводимости и тока смещения, всегда является замкнутым. Плотность полного тока 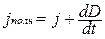 , где j – плотность тока в проводах, D – вектор электрического смещения поля в диэлектрике конденсатора. Полный ток через площадь S
, где j – плотность тока в проводах, D – вектор электрического смещения поля в диэлектрике конденсатора. Полный ток через площадь S
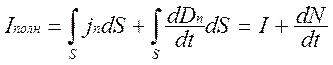 ,
,
где N –поток вектора электрического смещения через площадь S.
Второе основное положение теории Максвелла: переменное во времени электрическое поле вызывает появление вихревого магнитного поля
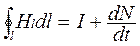
Таким образом. Максвелл показал, что электрическое и магнитное поля неразрывно связаны в единое электромагнитное поле, которое в частных статических ситуациях проявляется как электрическое или магнитное поле. На этой основе Максвелл создал единую теорию всех электрических и магнитных явлений.
Полная система уравнений теории включает, помимо двух основных положений, теорему Гаусса: поток вектора смещения через замкнутую поверхность равен заряду, охватываемому поверхностью
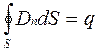 ;
;
Поток вектора магнитной индукции через замкнутую поверхность равен нулю (магнитных зарядов не существует)
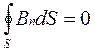
В систему уравнений входят также уравнения, включающие характеристики вещества – диэлектрическую и магнитную проницаемости, проводимость
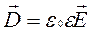
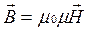
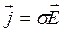
Теория Максвелла объяснила все открытые ранее явления электричества и магнетизма и предсказала существование электромагнитных волн. В настоящее время она является теоретической основой многих прикладных наук и технических направлений.
2. Из уравнений Максвелла были получены волновые уравнения для векторов Е и В. В случае однородной нейтральной непроводящей среды с постоянными проницаемостями ε и μ
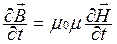 ,
, 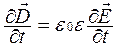
В результате математических преобразований из этих выражений получаются волновые уравнения
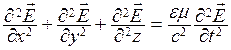 ,
,
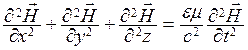 ;
;
Здесь вместо двух постоянных ε0 и μ0 введена одна постоянная с = 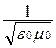 , причем коэффициент в правой части уравнений имеет смысл квадрата скорости волны, т.е. скорость электромагнитной волны
, причем коэффициент в правой части уравнений имеет смысл квадрата скорости волны, т.е. скорость электромагнитной волны
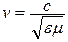
На практике впервые получил электромагнитные волны Генрих Герц в 1888 году. Герц не только экспериментально доказал существование электромагнитных волн, но впервые начал изучать их свойства – поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п. Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроводной связи (А. С. Попов, 1895 г.).
В начале двадцатого века многими учеными разных стран проводились опыты по определению скорости света, ее величина оказалась равной с. В вакууме с=3·10 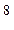 м/с.
м/с.
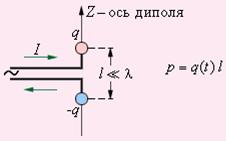
Для создания электромагнитной волны надо, чтобы существовало быстро изменяющееся электрическое или магнитное поле. Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент которого быстро изменяется во времени (рис.9.4). Это может быть небольшая антенна (в опыте Герца – вибратор), система ядро - электрон в атоме также представляет собой диполь (рис.9.4 а).
Вдоль оси диполя существует изменяющееся электрическое поле Е,котороепорождает вихревое магнитное поле В. Магнитное поле, в свою очередь, порождает вихревое электрическое поле и так далее. Этот процесс в виде электромагнитной волны распространяется вдоль оси Х со скоростью v, в направлении, перпендикулярном оси диполя (рис.9.4 б).
 а
а

б
Рис. 9.4
Обычно электромагнитную волну представляют в графическом виде (рис.9.5).

Рис.9.5
Электрическое и магнитное поля в любой момент времени нарастают или уменьшаются одновременно, т.е. колеблются синфазно во взаимно перпендикулярных плоскостях. Уравнения колебания векторов Е и В получены как решения дифференциального волнового уравнения
E = E0 cos (ωt – kx)
B = B0 cos (ωt – kx)
здесь k = ω/v или k = 2π/λ называется волновым числом.
В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают равноправно. Поэтому объемные плотности электрической и магнитной энергии равны друг другу: wэ = wм:
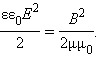
Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S , ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равная
ΔWэм = (wэ + wм)v SΔt
Скорость электромагнитной волны 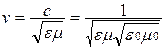
Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:
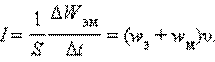
Подставляя выражения для wэ, wм и v, можно получить: 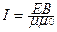
Поток энергии в электромагнитной волне можно задавать вектором 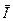 ,
,
направление которого совпадает с направлением распространения волны, а модуль равен EB / μμ0. Этот вектор называют вектором Пойнтинга.
Плотность потока энергии в СИ измеряется в Вт/м2.
3. Электромагнитные волны классифицируются по длине волны λ или связанной с ней частотой υ волны. Спектром электромагнитных волн называется полоса частот электромагнитных волн, существующих в природе.
Электромагнитные волны излучаются антеннами или атомами вещества. Длина волны излучения составляет обычно половину размера излучателя, поэтому спектр электромагнитного излучения достаточно широк (рис.9.5).
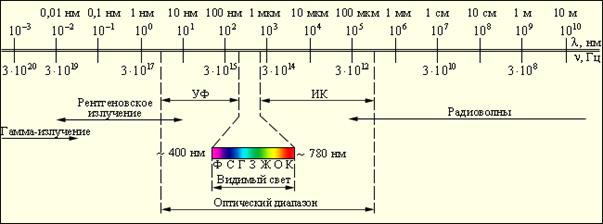
Рис.9.5
.
Спектр электромагнитного излучения в порядке увеличения частоты составляют:
- радиоволны;
- инфракрасное излучение;
- оптическое излучение;
- рентгеновское излучение;
- гамма-излучение.
Между различными участками электромагнитного спектра нет резких границ.
Радиоволны излучаются и принимаются антеннами и делятся на:
• Длинные волны в интервале длин волн от десятков км до 1км (частота в диапазоне от 3 кГц до 300кГц);
• Средние волны в интервале длин волн от1км до 100м (частота в диапазоне 3 105 Гц – 3МГц);
• Короткие волны в интервале длин волн от 100м до 10м (частота в диапазоне 3106Гц-3107Гц);
• Ультракороткие волны (УКВ) с длиной волны меньше 10м (частота больше 3107гц=30Мгц).
Волны с длиной волны меньше, чем 1м (частота больше 300мгц) называются микроволнами или волнами сверхвысоких частот (СВЧ - волны).
Оптическая область спектра включает инфракрасное (ИК) излучение, видимый свет и ультрафиолетовое (УФ) излучение. Оптическое излучение испускается при переходах в атомах электронов внешних орбиталей.
Оптический спектр занимает диапазон длин электромагнитных волн в интервале от 2·10-6м= 2мкм до 10-8м=10нм (по частоте от1,5·1014Гц до 3·1016Гц). Верхняя граница оптического диапазонаопределяется длинноволновой границей инфракрасного диапазона,анижняя коротковолновой границей ультрафиолета.
Рентгеновское излучение возникает при торможении быстрых заряженных частиц (электронов, протонов и пр.), а также в результате переходов электронов внутренних электронных оболочек атомов. Рентгеновское излучение составляют электромагнитные волны с длиной от 50 нм до 10-3нм.
Гамма-излучение является следствием явлений, происходящих внутри атомных ядер, а также в результате ядерных реакций. Гамма излучение составляют электромагнитные волны с длиной волны меньше 10-2 нм.
ЛЕКЦИЯ 10
Тема:Фотометрические характеристики света. Законы геометрической оптики.
Дата добавления: 2015-09-18; просмотров: 804;
