Действие магнитного поля на контур с током
Выясним, как ведет себя контур с током в однородном магнитном поле 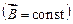 . Согласно (1.5) на каждый элемент контура
. Согласно (1.5) на каждый элемент контура 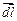 действует сила
действует сила
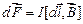 .
.
Результирующая этих сил
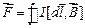 .
.
Вынеся постоянные величины 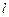 и
и 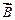 за знак интеграла, получим:
за знак интеграла, получим:
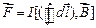 .
.
Интеграл 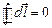 , поэтому
, поэтому 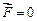 . Таким образом, результирующая сила, действующая на контур с током в однородном магнитном поле, равна нулю. Это справедливо для контуров любой формы (в том числе неплоских) при произвольном расположении контура относительно направления
. Таким образом, результирующая сила, действующая на контур с током в однородном магнитном поле, равна нулю. Это справедливо для контуров любой формы (в том числе неплоских) при произвольном расположении контура относительно направления 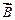 . Существенной для равенства нулю результирующей силы является лишь однородность поля.
. Существенной для равенства нулю результирующей силы является лишь однородность поля.
Предположим, что контур имеет прямоугольную форму. Рассмотрим два случая.
1) Пусть 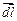 перпендикулярен
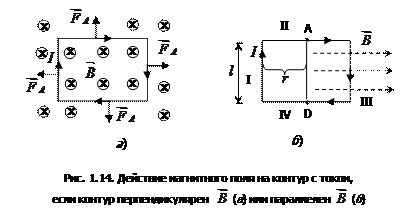
перпендикулярен 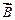 , т.е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, показаны на рис. 1.14, а.
, т.е. любой элемент контура перпендикулярен силовым линиям. Cилы Ампера, действующие на каждый прямолинейный участок контура, показаны на рис. 1.14, а.
Если контур с током расположен перпендикулярно силовым линиям, то действие поля выражается в сжатии и растяжении и контура. Если же контур состоит из упругого проводника, то внешнего изменения положения в пространстве не будет.
2) Пусть 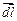 параллелен
параллелен 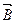 , т.е. нормаль плоскости контура перпендикулярна вектору магнитной индукции (рис.1,14, б).
, т.е. нормаль плоскости контура перпендикулярна вектору магнитной индукции (рис.1,14, б).
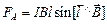 ,
,
тогда силы Ампера на каждом участке, определяются следующим образом:
I. 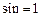 ,
, 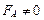 , сила направлена от нас;
, сила направлена от нас;
II, IV. 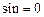 ,
, 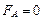 , т.е. на элемент контура с током, лежащим вдоль силовых линий,
, т.е. на элемент контура с током, лежащим вдоль силовых линий, 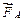 не действует;
не действует;
 III.
III. 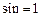 ,
,  , сила направлена к нам.
, сила направлена к нам.
Если контур с током закрепить в точках  и
и 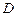 , то при таком расположении его в магнитном поле он будет вращаться, т.е. на него будет действовать момент силы
, то при таком расположении его в магнитном поле он будет вращаться, т.е. на него будет действовать момент силы 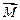 .
.
Пусть 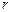 – плечо силы
– плечо силы 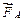 (рис. 1.14, б). Если
(рис. 1.14, б). Если 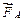 перпендикулярна
перпендикулярна 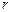 , тогда
, тогда 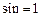 и момент силы, действующий на I (или III) участок контура
и момент силы, действующий на I (или III) участок контура
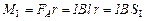 ,
,
где 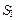 – площадь между линией AD и участком тока I (или III).
– площадь между линией AD и участком тока I (или III).
Поскольку на каждую из противоположных сторон контура (участки I и III) действует самостоятельная сила Ампера, то в качестве площади для суммарного момента сил принимается не половина площади контура, а вся. Тогда понятие магнитного момента контура с током вводится как собственная характеристика контура, которая численно равна 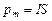 , где
, где 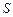 – площадь контура. Направление магнитного момента задается нормалью контура с током
– площадь контура. Направление магнитного момента задается нормалью контура с током 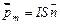 .
.
Полный момент силы, действующий на контур с током в магнитном поле, численно равен: 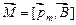 .
.
Модуль вектора 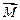 равен:
равен: 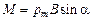 .
.
Для того чтобы угол 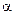 между векторами
между векторами 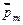 и
и 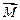 увеличить на
увеличить на 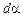 , нужно совершить против сил, действующих на контур в магнитном поле, работу
, нужно совершить против сил, действующих на контур в магнитном поле, работу
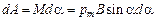 . (1.16)
. (1.16)
Возвращаясь в первоначальное положение, контур может вернуть затраченную на его поворот работу, совершив ее над каким-нибудь телом. Следовательно, работа (1.16) идет на увеличение потенциальной энергии 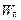 , которой обладает контур с током в магнитном поле:
, которой обладает контур с током в магнитном поле:
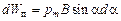 .
.
Интегрируя, находим:
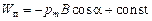 ,
,
полагая 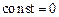 , получаем:
, получаем:
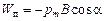 .
.
Параллельная ориентация векторов 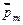 и
и 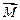 отвечает минимуму энергии и, следовательно, положению устойчивого равновесия контура.
отвечает минимуму энергии и, следовательно, положению устойчивого равновесия контура.
Дата добавления: 2015-09-18; просмотров: 2778;
