Намагниченность магнетика
В дальнейшем будем различать макроскопические токи, т.е. электрические токи, протекающие по проводникам в электрических цепях, и микроскопические токи, обусловленные движением электронов в атомах и молекулах.
Намагничивание постоянных магнитов является следствием существования в них микротоков.
Для количественного описания магнитных свойств вещества ввели векторную величину – намагниченность, равную векторной сумме магнитных моментов 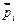 атомов, которые находятся в единице объема вещества:
атомов, которые находятся в единице объема вещества:
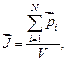
где 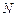 – число атомов, находящихся в объеме
– число атомов, находящихся в объеме 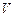 .
.
Вектор индукции магнитного поля 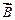 характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Следовательно, магнитное поле в веществе складывается из двух полей:
характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Следовательно, магнитное поле в веществе складывается из двух полей:
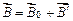 ,
,
где 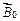 – индукция магнитного поля, создаваемого макроскопическими токами, без учета свойств вещества (например, в вакууме);
– индукция магнитного поля, создаваемого макроскопическими токами, без учета свойств вещества (например, в вакууме); 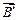 – индукция магнитного поля, создаваемого микроскопическими токами.
– индукция магнитного поля, создаваемого микроскопическими токами.
Магнитное поле макроскопических токов описывается вектором напряженности магнитного поля 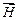 . Вектор
. Вектор 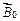 связан с вектором
связан с вектором 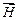 следующим соотношением:
следующим соотношением:
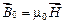 .
.
Для описания магнитного поля микротоков рассмотрим вещество (магнетик) в виде цилиндра площадью сечения 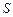 и длиною
и длиною 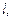 находящегося в однородном магнитном поле, вектор индукции которого
находящегося в однородном магнитном поле, вектор индукции которого 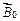 (рис. 2.2, а). Вектор индукции направлен вдоль оси цилиндра от нас.
(рис. 2.2, а). Вектор индукции направлен вдоль оси цилиндра от нас.
Если рассматривать любое сечение цилиндра, перпендикулярное его оси (рис. 2.2, б), то во внутренних участках сечения магнетика микротоки атомов направлены навстречу друг другу и взаимно компенсируются. Нескомпенсированными остаются лишь микротоки, выходящие на боковую поверхность цилиндра.
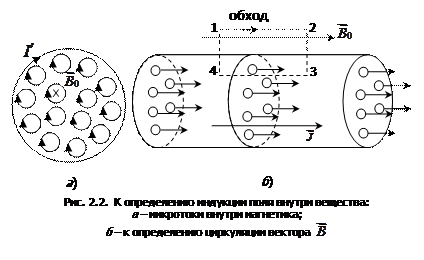
Ток, текущий по боковой поверхности цилиндра, создает магнитное поле, индукцию которого 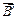 можно определить по формуле для соленоида, полагая, что он состоит из одного витка:
можно определить по формуле для соленоида, полагая, что он состоит из одного витка:
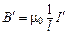 , (2.3)
, (2.3)
где 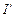 – микротоки, протекающие по боковой поверхности цилиндра;
– микротоки, протекающие по боковой поверхности цилиндра; 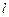 – длина соленоида.
– длина соленоида.
Магнитный момент, создаваемый всеми микротоками соленоида
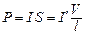 ,
,
где 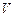 – объем соленоида.
– объем соленоида.
Выражая магнитный момент 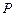 через намагниченность, получаем
через намагниченность, получаем 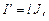 или после подстановки значения
или после подстановки значения 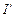 в формулу (2.3) получим:
в формулу (2.3) получим:
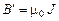 или в векторной форме
или в векторной форме 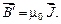
Учитывая значения 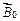 и
и 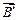 , индукцию поля, создаваемого макро- и микротоками, можно записать в таком виде:
, индукцию поля, создаваемого макро- и микротоками, можно записать в таком виде:
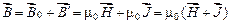 . (2.4)
. (2.4)
Экспериментально установлено, что намагниченность 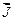 пропорциональна напряженности поля, которое ее вызывает, т.е.
пропорциональна напряженности поля, которое ее вызывает, т.е.
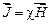 , (2.5)
, (2.5)
где 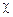 – коэффициент пропорциональности, называемый магнитной восприимчивостью.
– коэффициент пропорциональности, называемый магнитной восприимчивостью.
Используя выражение (2.5), результирующую индукцию поля в веществе (2.4) можно записать в виде:
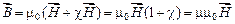 . (2.6)
. (2.6)
Безразмерная величина 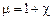 называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества.
называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества.
Формула (2.6) устанавливает связь между индукцией магнитного поля 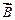 внутри вещества и напряженностью внешнего поля
внутри вещества и напряженностью внешнего поля 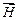 .
.
2.3. Теоремы о циркуляции векторов 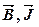 и
и 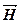
В случае определения индукции магнитного поля в вакууме было получено выражение циркуляции вектора 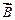 в таком виде:
в таком виде:
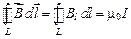 . (2.7)
. (2.7)
Микротоки в вакууме равны нулю. В случае определения индукции поля в веществе может быть использовано выражение (2.6). С учетом того, что кроме макро- присутствуют и микроскопические токи, выражение (2.7) принимает вид:
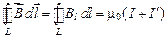 .
.
Вектор 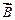 характеризует поле макро- и микроскопических токов.
характеризует поле макро- и микроскопических токов.
Определим циркуляцию вектора 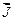 . Для этого проведем замкнутый контур прямоугольной формы, одна из сторон которого находится внутри вещества (рис. 2.2., б):
. Для этого проведем замкнутый контур прямоугольной формы, одна из сторон которого находится внутри вещества (рис. 2.2., б):
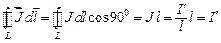 .
.
Мы учли выражение 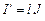 .
.
Таким образом, 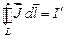 . Источником вектора
. Источником вектора 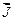 являются микротоки.
являются микротоки.
Для определения циркуляции вектора 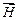 воспользуемся взаимосвязью между векторами
воспользуемся взаимосвязью между векторами 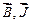 и
и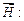
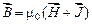 , откуда
, откуда 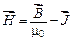 .
.
В таком случае
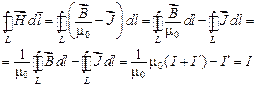
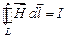 ,
,
т.е. источником вектора 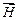 являются макроскопические токи.
являются макроскопические токи.
Дата добавления: 2015-09-18; просмотров: 1725;
