Движение заряженных частиц в магнитном поле

Считаем, что магнитное поле однородно и на частицы не действуют электрические поля. Рассмотрим три возможных случая.

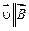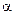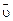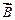1. – заряженная частица движется в магнитном поле вдоль линий магнитной индукции (угол между векторами и равен 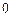или 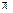). Сила Лоренца равна нулю. Магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

2. 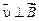– заряженная частица движется в магнитном поле перпендикулярно линиям магнитной индукции ( 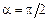). Сила Лоренца 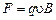постоянна по модулю и перпендикулярна вектору скорости. Частица будет двигаться по окружности радиусом 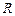с центростремительным ускорением 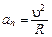. Из второго закона Ньютона 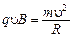получаем радиус окружности 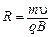и период вращения .

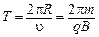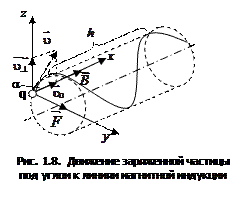
3. Заряженная частица движется под углом 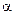к линиям магнитной индукции. Тогда движение частицы можно представить в виде суммы двух движений (рис. 1.8):

а) равномерного прямолинейного движения вдоль поля со скоростью ;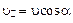

б) равномерного движения по окружности в плоскости, перпендикулярной полю, со скоростью .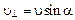

Суммарное движение будет движением по спирали, ось которой параллельна магнитному полю. Шаг винтовой линии 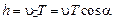, где 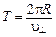– период вращения частицы, и 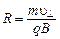. Тогда

.

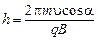Если магнитное поле неоднородно и заряженная частица движется под углом к линиям магнитного поля в направлении возрастания поля, то величины 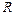и 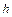уменьшаются с ростом 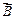. На этом основана фокусировка заряженных частиц магнитным полем.